Question 1203682: The hourly wage of some Toyota assembly line workers increased annually by the same percentage if their wage went from 7.10 to 20.08 in 12 years what is the doubling time
Found 3 solutions by ikleyn, Edwin McCravy, math_tutor2020:
Answer by ikleyn(52832)   (Show Source):
You can put this solution on YOUR website! .
The hourly wage of some Toyota assembly line workers increased annually by the same percentage
if their wage went from 7.10 to 20.08 in 12 years what is the doubling time
~~~~~~~~~~~~~~~~~~~~~
According to the problem, for the annual salary we have this exponential equation
y = 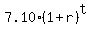 , where "t" denotes years from the starting moment.
We want to find (1+r), the coefficient of growth.
At t= 12 we have
20.08 =  .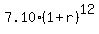
Divide both sides by 7.10
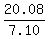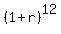 =  , or
2.828169014 = .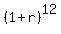
Take logarithm base 10 of both sides
log(2.828169014) = 12*log(1+r)
log(1+r) = 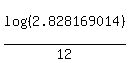 = 0.037625447.
Hence,
1+r = 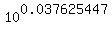 = 1.09049944.
Thus we just found out the coefficient of growth.
To find the doubling period, we shoud find "t" from this equation
2 =  , or
2 =  .
Again, take logarithm base 10 of both sides
log(2) = t*log(1+r).
We just found out the value of log(1+r) above: it is 0.037625447.
Therefore, the doubling time is t = 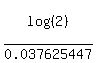 = 8.000702 years,
which we can round to 8 years.
ANSWER. The doubling period is 8 years.
Solved.
Answer by Edwin McCravy(20060)  (Show Source):
Answer by math_tutor2020(3817)  (Show Source):
|
|
|
