|
Question 1203670: A line’s equation is given in point-slope form: y=(-2/9)(x+9)+1
This line’s slope is -2/9
What is a point on this line that is apparent from the given equation?
*I've tried (0,-1), (-9/2,0), (-2,-5/9) but all these answers are wrong.
Found 3 solutions by josgarithmetic, MathTherapy, greenestamps:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! Equation as given or shown,  . .
The apparent point may seem more easily apparant this way:

which is point-slope form (almost) and there is a point to read from this as (-9,1).
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
line’s equation is given in point-slope form: y=(-2/9)(x+9)+1
This line’s slope is -2/9
What is a point on this line that is apparent from the given equation?
*I've tried (0,-1), (-9/2,0), (-2,-5/9) but all these answers are wrong
Point-slope form of a linear equation:  For y =
For y = 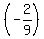 (x + 9) + 1, we need to subtract 1 from both sides of the equation.
When done, y = (x + 9) + 1, we need to subtract 1 from both sides of the equation.
When done, y = 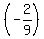 (x + 9) + 1 becomes: (x + 9) + 1 becomes:  Compared to:
Compared to:  , we see that: , we see that:
 , and also: , and also:  Therefore, (x1, y1) = (- 9, 1). This is your point on the line, from the given equation.
Therefore, (x1, y1) = (- 9, 1). This is your point on the line, from the given equation.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!

There is no need to move the 1 to the left to answer the question.
The point on the line that is "apparent" from the given equation is the point where the value of x makes "(-2/9)(x+9)" equal to 0 (i.e., x=-9), in which case the y value will be (-2/9)(0)+1 = 0+1 = 1.
ANSWER: (x,y) = (-9,1)
|
|
|
| |