SOLUTION: Assume the probability of a boy being born is the same as the probability of a girl being born. Find the probability that a family with four children will have the given compositi

There are two possible outcomes on each birth, boy (B) or girl (G).  So for 4 children, the number of total possible outcomes is  =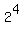 



This is small enough to enumerate all of them.  After that, you

should be able to easily complete the problems (I'll do the first

part as a template).



1  BBBB

2  BBBG

3  BBGB

4  BBGG

5  BGBB

6  BGBG

7  BGGB

8  BGGG

9  GBBB

10 GBBG

11 GBGB

12 GBGG

13 GGBB

14 GGBG

15 GGGB

16 GGGG



(1) P(two boys and two girls) = 6/16 = 3/8 

To see this, notice the number of outcomes with 2B and 2G is 6 (lines 4,6,7,10,11, and 13).  The probability is the count of the outcomes of interest, divided by the total number of possible outcomes.total possible outcomes.



==

As an Algebraic solution, you would use combinations.  The probability of 2 boys and 2 girls is equivalent to the probability of 2 boys out of 4 children total: 

    Using nCr = (n!)/((n-r)!r!)  ("n choose r")  

  P(2 boys and 2 girls) = P(2 boys out of 4 children) = 4C2 / 16 = 6/16 = 3/8

==



The other parts are solved similarly, just adjust how you select the outcomes of interest (or compute the combinations).