Question 1203648: A series of 384 consecutive odd integers has a sum that is a perfect fourth power of a positive integer. Find the smallest possible sum for this series
Found 3 solutions by MathLover1, ikleyn, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
here is a link to solution:
https://www.algebra.com/algebra/homework/Sequences-and-series/Sequences-and-series.faq.question.898860.html
Answer by ikleyn(52890)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A series of 384 consecutive odd integers has a sum that is a perfect fourth power of a positive integer.
Find the smallest possible sum for this series
~~~~~~~~~~~~~~~~~~~~~~~~~~
It is a Math Olimpiad level problem. So I will write the solution as if I talk with
an advanced level student, whose level corresponds to the problem's level.
In other words, I will point the major ideas accurately, but will not go in details.
1. The solution starts from a remarkable formula for the sum of the first n odd integer numbers
 = 1 + 3 + 5 + 7 + . . . + (2n-1) = = 1 + 3 + 5 + 7 + . . . + (2n-1) =  , (1)
which is valid for any natural "n".
2. The series under the question (the arifmetic progression) can start from a positive first term;
in this case it lies entirely in the domain of positive integer numbers.
It also can partly lie in the domain of negative integer numbers and partly in the domain
of positive integer numbers. The condition does not prohibit it . . .
But it can not lie entirely in the domain of negative integer numbers, since the sum must be
positive number.
3. If the progression starts from some positive number, let say
S = (2k+1) + (2k+3) + . . . + (2n-1),
then its sum is
S = , (1)
which is valid for any natural "n".
2. The series under the question (the arifmetic progression) can start from a positive first term;
in this case it lies entirely in the domain of positive integer numbers.
It also can partly lie in the domain of negative integer numbers and partly in the domain
of positive integer numbers. The condition does not prohibit it . . .
But it can not lie entirely in the domain of negative integer numbers, since the sum must be
positive number.
3. If the progression starts from some positive number, let say
S = (2k+1) + (2k+3) + . . . + (2n-1),
then its sum is
S =  - -  , (2)
according to the formula (1). (Indeed, in this case S = , (2)
according to the formula (1). (Indeed, in this case S =  - - 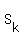 , and then the formula (1) works).
If the progression starts from some negative integer number and partly lies in the negative domain
and partly in the positive domain, the same formula (2) works.
In this case the positive addend , and then the formula (1) works).
If the progression starts from some negative integer number and partly lies in the negative domain
and partly in the positive domain, the same formula (2) works.
In this case the positive addend  corresponds to the part of the series, which is in positive
domain, while the negative addend corresponds to the part of the series, which is in positive
domain, while the negative addend 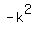 corresponds to the part of the series, which is in negative domain.
So, the formula (2) works for any of the two admitted cases.
4. We want the sum of the series be the fourth degree of some integer "d". It means that the equation corresponds to the part of the series, which is in negative domain.
So, the formula (2) works for any of the two admitted cases.
4. We want the sum of the series be the fourth degree of some integer "d". It means that the equation
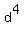 = =  - -  , (3)
must be hold.
5. Decompose , (3)
must be hold.
5. Decompose  - -  as (n+k)*(n-k). Then the equiation (3) becomes as (n+k)*(n-k). Then the equiation (3) becomes
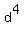 = (n+k)*(n-k). (4)
6. Now notice that n-k must be equal to 384, the number of the terms in the series.
The number 384 has the decomposition into the product of prime numbers 2 and 3:
384 = 3*128 = = (n+k)*(n-k). (4)
6. Now notice that n-k must be equal to 384, the number of the terms in the series.
The number 384 has the decomposition into the product of prime numbers 2 and 3:
384 = 3*128 = 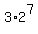 .
So, it should be .
So, it should be
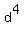 = = 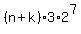 . (5)
In order for the equality (5) was possible, the factor (n+k) must complement . (5)
In order for the equality (5) was possible, the factor (n+k) must complement 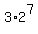 to the full fourth degree integer.
The minimal such complement is n+k = to the full fourth degree integer.
The minimal such complement is n+k = 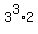 = 27*2 = 54.
It gives us two equations for n and k:
n - k = 384 (6) (as was noticed above), and
n + k = 54 (7)
From these equations, it is easy to get
n = 219, k = -165.
7. Thus we get that the progression starts from 2*(-165)+1 = -329 and lasts till 2*219-1 = 437.
So, the progression partly lies in the negative and partly in positive domain.
Answer. Arithmetic progression
-329, -327, - 325, . . . , 437
(first term is -329, the common difference is 2, the last term is 437, the number of terms is 384) has the sum 20736 = = 27*2 = 54.
It gives us two equations for n and k:
n - k = 384 (6) (as was noticed above), and
n + k = 54 (7)
From these equations, it is easy to get
n = 219, k = -165.
7. Thus we get that the progression starts from 2*(-165)+1 = -329 and lasts till 2*219-1 = 437.
So, the progression partly lies in the negative and partly in positive domain.
Answer. Arithmetic progression
-329, -327, - 325, . . . , 437
(first term is -329, the common difference is 2, the last term is 437, the number of terms is 384) has the sum 20736 = 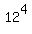 .
And this progression provides the minimal positive sum which is the fourth degree of the integer number.
Check. The sum of the progression = .
And this progression provides the minimal positive sum which is the fourth degree of the integer number.
Check. The sum of the progression = 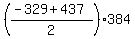 = 20736. = 20736.
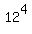 = 20736. ! Correct !
The number of terms in the progression = = 20736. ! Correct !
The number of terms in the progression = 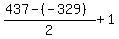 = 384. ! Correct ! = 384. ! Correct !
******************************
* * * Completed and solved ! * * *
******************************
I solved this problem several years ago at this forum.
That my solution is under the link
https://www.algebra.com/algebra/homework/Problems-with-consecutive-odd-even-integers/Problems-with-consecutive-odd-even-integers.faq.question.1122929.html
For your convenience, I copy-pasted that solution here.
Enjoy ( ! )
Answer by greenestamps(13209)   (Show Source): (Show Source):
|
|
|