SOLUTION: Could you please help me with this Calculus problem? I am finding this problem hard to solve. After a few steps, I am stuck and don't know how to proceed to find the derivative.

h(x) = 



The product rule can be applied:



If  h(x) = A(x)B(x) then 

 

    h'(x) = A(x)B'(x) + B(x)A'(x)



Choosing A(x) = (3x-12) and B(x) = 



 A'(x) = 3



Unfortunately, B'(x) will be messy:

 B'(x) =  





Now you have:

   h'(x) =   + 





Expand the first term, combine like-terms, and pull out , and you should get:



   h'(x) = 



[ Sometimes writing  as x^(1/2) makes the workout easier. ]



---

EDIT 9/14/23:  tutor greenestamps answer is missing a factor of 

 

Formally speaking, to solve such problem successfully, you need to know pre-requisites.
The pre-requisites are:

    (a) knowing what a derivative is, in general;

    (b) knowing derivatives of table functions;

    (c) knowing the rule of taking derivative for a product of two functions

            ((f(x)*(g(x))' = f'(x)*g(x) + f(x)*g'(x)

        and for a product of three functions

            (f(x)*g(x)*h(x))' = f'(x)*g(x)*h(x) + f(x)*g'(x)*h(x) + f(x)*g(x)*h'(x).


Formally, that is all.


But, to be honest, in addition to it, you should have another pre-requisite,
which is the developed technique of solving more simple problems.


To develop such a technique, solve  a series of more simple problems,
listed below.  Take the derivatives of these functions

    (a)  ;

    (b)  ;

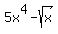    (c)  .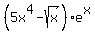


As soon as you complete these problems, you will be ready to work on your
problem in the post.  Then it will be not so difficult exercise for you.