SOLUTION: what is the coefficient of the 5th term of the expansion of (2x^2 + 3y^3)^10 how about the sum of exponents of the terms in expansion

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: what is the coefficient of the 5th term of the expansion of (2x^2 + 3y^3)^10 how about the sum of exponents of the terms in expansion       Log On


   

Question 1203588: what is the coefficient of the 5th term of the expansion of (2x^2 + 3y^3)^10 how about the sum of exponents of the terms in expansion

Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

To find the coefficient of the 5th term in the expansion of %282x%5E2%2B+3y%5E3%29%5E10, we need to use the binomial theorem.
The general term in the expansion of %282x%5E2%2B+3y%5E3%29%5E10 is given by:

T%28r%2B1%29+=+C%2810%2C+r%29+%2A+%282x%5E2%29%5E%2810-r%29+%2A+%283y%5E3%29%5Er

where C%2810%2C+r%29 is the binomial coefficient of 10 and r, given by:

C%2810%2C+r%29+=+10%21+%2F+%28r%21+%2A+%2810+-+r%29%21%29

To find the 5th term, we need to substitute r+=+4, since the first term has r+=+0. Therefore, the 5th term is:

T%285%29+=+C%2810%2C+4%29+%2A+%282x%5E2%29%5E%2810-4%29+%2A+%283y%5E3%29%5E4
= C%2810%2C+4%29+%2A+%282x%5E2%29%5E6+%2A+%283y%5E3%29%5E4
= 210+%2A+64x%5E12+%2A+81y%5E12
= 1088640x%5E12%2Ay%5E12

Therefore, the coefficient of the 5th term in the expansion of %282x%5E2+%2B+3y%5E3%29%5E10 is 1088640.


Answer by greenestamps(13209) About Me  (Show Source):
You can put this solution on YOUR website!


It is not clear what you are asking when, at the end of your post, you say "how about the sum of exponents of the terms in expansion"....

The first term of the expansion is %282x%5E2%29%5E10, so the exponent on that term is 2*10 = 20.

The second term includes factors of 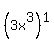%282x%5E2%29%5E9 and %283x%5E3%29%5E1, so the exponent on that term is (2*9)+(3*1) = 21.

On the next terms the sums of the exponents will be 22, then 23, then 24...

The last term is 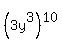%283y%5E3%29%5E10, so the exponent on that term is 3*10 = 30.

So the sums of the exponents on successive terms of the expansion will be 20, 21, 22, ..., and 30.