Question 1203586: Nevada license plates consist of 6 letters/numbers in the following format: 123* A45. That is, 3 numbers, followed by a letter, then 2 more numbers. Note that numbers may be repeated on each license plate.
What is the probability that a randomly selected license plate does not contain a vowel, given the first number is even?
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 21/26
Reason:
There are 5 vowels a, e, i, o, and u.
The remaining 26-5 = 21 letters are consonants.
------------------------------
A longer method is shown below.
We need to find out how many ways there are to get a license plate with an even number in the 1st slot.
Even single digit numbers = {0,2,4,6,8}
There are 5 values here.
We have 5 choices for slot 1, then 10 choices for slot 2 and for slot 3.
Then we have 26 choices for slot 4 because this is where the letters go.
We have 10 choices each for slots 5 and 6.
Overall we have 5*10*10*26*10*10 = 1,300,000 different license plates where the first digit is an even number.
We'll have 5*10*10*(26-5)*10*10 = 5*10*10*21*10*10 = 1,050,000 different plates where a vowel does not show up. The 26-5 portion is us kicking out the 5 vowels {a,e,i,o,u}
Divide the two results.
Since a lot of things will cancel, I'll divide the unevaluated expressions to show those cancellations.


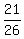
We end up with the answer 21/26 we got earlier.
|
|
|