Question 1203579: An internet search engine looks for a keyword in 9 databases, searching them in a random order. Only 5 of these databases contain the given keyword. Find the probability that it will be found in at least 2 of the first 4 searched databases. Round to 4 decimal places.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll assume that it is not going to search the same database twice.
The denominator will be C(9,4) = 126
There are 4 that don't contain the password and 5 that do.
We find the probability of the complement event, that the first 4 searches
do not find at least 2 that contain the password at least twice. That means
that either it finds none that contain it, or it finds exactly 1 that contains
it.
The number when exactly 0 contain the password is 1 way. Choose all 4 that don't
contain the password. C(4,4)=1
The number when exactly 1 contains the password.
For each of the C(4,3)=4 choices of 3 that don't contain the password,
we choose 1 that does in C(5,1)=5 ways. That's (4)(5)=20 ways.
That's 1+20 = 21 unacceptable ways.
So the probability of the complement event is 21/126 = 1/6
So the probability of the desired event is 1-1/6 or 5/6.
Edwin
Answer by ikleyn(52925)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An internet search engine looks for a keyword in 9 databases,
searching them in a random order.
Only 5 of these databases contain the given keyword.
Find the probability that it will be found in at least 2 of the first 4 searched databases.
Round to 4 decimal places.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For me, it is easier to reformulate the problem.
I will consider the databases as balls marked by letters G (=good) if they contain the keyword,
or B (=bad) if they do not contain.
So, I have 5 balls marked G and 4 balls marked B.
+--------------------------------------------------------------------------+
| For clarity, I consider all 9 balls as different (distinguishable), |
| but the order of balls in my selections does not matter, |
| as in classic combinations. Only their amounts do matter. |
+--------------------------------------------------------------------------+
I will consider the first 4 searched databases as box N (= oNe) and the rest 5 databases
as box T (= Two).
So, now I have 5 balls G and 4 balls B.
I also have box N (meaning first 4 searched databases) and box T (meaning the rest 5 databases).
An experiment is placing arbitrary (= randomly) 4 of 9 balls into box N
(and placing the rest 5 balls in box T just without choice).
The question is to find the probability of getting 2, or 3, or 4 balls G in box N.
Total of possible different combinations in box N is 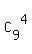 = 126.
It is the size of the space of events in my consideration.
The number of combinations getting 2 balls G in box N is = 126.
It is the size of the space of events in my consideration.
The number of combinations getting 2 balls G in box N is 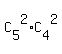 = 10*6 = 60
(we combine 2G of 5G and 2B of 4B in box N)
The number of combinations getting 3 balls G in box N is = 10*6 = 60
(we combine 2G of 5G and 2B of 4B in box N)
The number of combinations getting 3 balls G in box N is 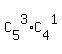 = 10*4 = 40
(we combine 3G of 5G and 1B of 4B in box N)
The number of combinations getting 4 balls G in box N is = 10*4 = 40
(we combine 3G of 5G and 1B of 4B in box N)
The number of combinations getting 4 balls G in box N is 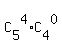 = 5*1 = 5
(we combine 4G of 5G and 0B of 4B in box N)
Now the answer to the problem's question is
P = = 5*1 = 5
(we combine 4G of 5G and 0B of 4B in box N)
Now the answer to the problem's question is
P = 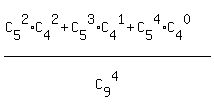 = = 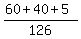 = =  = =  .
ANSWER. The probability is .
ANSWER. The probability is  . .
Solved.
|
|
|