Question 1203536: Calculate selling price of a house if:
They paid 21082.00 down
payments are 682.00 per month for 30 years
interest rate 6.6% is compounded monthly
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! the amount of the loan is 106786.28
add to that the down payment of 21082 to get a total sale price of 127868.28.
here are the results from the calculator that i used.
the inputs to this calculator were:
present value = -
future value = 0
number pf time periods = 30 * 12 = 360 months.
payment amount per time period = -682
interest rate per time period = 6.6% / 12 = .55%
payments are made at the end of each time period.
i clicked on present value.
the calculator came back with a present value of 106786.28.
that was the amount of the loan.
the calculator that i used can be found at https://arachnoid.com/finance/
Answer by ikleyn(52805)  (Show Source):
You can put this solution on YOUR website! .
Calculate selling price of a house if:
They paid 21082.00 down
payments are 682.00 per month for 30 years
interest rate 6.6% is compounded monthly
~~~~~~~~~~~~~~~~~~~~~~~~~
This my solution goes second after the solution by @Theo.
@Theo used an online calculator in his solution.
Since this web-site is to teach Math, the expected solution should be mathematical.
So, I present here a standard mathematical solution.
Calculator can be used as a secondary tool for verification.
Then the sequence of steps would be normally educative.
In this problem, we are given the monthly payment for the loan;
the annual interest rate and the duration of the loan.
Having this input information, we can find the loaned amount.
Use the formula for the monthly payment for a loan
M =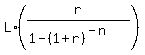 
where L is the loan amount; r is the effective interest rate per month;
n is the number of payments (same as the number of months); M is the monthly payment.
From this formula, express for the loan amount
L =  .
In this problem M = $682; r =  , n = 30*12 = 360 monthly payments.
Substitute these values into the formula and get for the maximum loan amount
L =  = $106,786.28.
To find the celling price of the house, we should add the down payment to this value
the celling price = $106,786.28 + $21,082.00 = $127,868.281
ANSWER. The selling price of the house is $127,868 (rounded to the closest dollar).
Solved.
Notice that my numbers precisely coincide with the numbers in the post by @Theo, so you can consider it as a check.
---------------------------
In such calculations, it is important to avoid intermediate rounding.
Rounding can be done at the end, only.
Intermediate rounding is PROHIBITED, since it leads to wrong answer.
Also, a calculator should provide the necessary precision.
I use MS Excel in my computer. It works with 15 decimals in mantissa
and provides the necessary precision.
I simply copy-paste my numerical formula into Excel spreadsheet and get the answer in one click.
Many standard online calculators provide the necessary precision.
You may use, for example, this free-of-charge online calculator
https://www.calculatorsoup.com/calculators/financial/loan-calculator.php
It is reliable, has convenient user-friendly interface, has complete instructions and descriptions,
provides the necessary precision and was checked million times. You may use it to check my/your calculations.
//////////////////////////////////////////
There is another (= one more) reason why I produced and placed my solution here.
@Theo' posts used visual plots to support his solutions.
These plots were integral inseparable part of his solutions.
But some time ago, Theo left this forum and stopped supporting web-site with his plots.
As a result, you see now some colored spots in his posts, where his plots should be.
Due to this reason, @Theo's posts lost their educational meaning and value.
Therefore, I create my posts with my own mathematical solutions
to replace @Theo' solutions and provide meaningful mathematical content.
|
|
|
