Question 1203532: suppose that milk is shipped to retail outlets in boxes that hold 16 milk containers .One particular box which happens to contain 6 underweight containers is opened for inspection and 5 containers are choosen at random interpret the distribution of the number of underweight milk containers in the sample chosen by the inspector .Also comment on the expected value value of the distribution .What is the probability that exact 2 underweight containers are selected
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i think this is goiing to be a binomial distriution type problem.
there are 16 containers in the box, 6 of which are defective.
probability of any one container being defective is 6/16.
you randomly choose 5 out of the 16.
the binomial distibution formula is p(x) = p^x * (1-p)^(n-x) * c(n,x)
the probability that exactly 2 out of the 5 are defective would be:
p(2) = (6/16)^2 * (1 - 6/16)^(5-2) * c(5,2) = .3433227539.
the total probability should be 1, as shown in the following excel file display.

Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose that milk is shipped to retail outlets in boxes that hold 16 milk containers .
One particular box which happens to contain 6 underweight containers is opened for inspection
and 5 containers are chosen at random.
(a)  Find the distribution of the number of underweight milk containers Find the distribution of the number of underweight milk containers
in the sample chosen by the inspector.
(b) Also  find on the expected value value of the distribution. find on the expected value value of the distribution.
(c) What is the probability that exact 2 underweight containers are selected
~~~~~~~~~~~~~~~~~~~~
The solution in the post by @Theo is INCORRECT.
The CONCEPTUAL ERROR which he made is that this distribution IS BINOMIAL.
Actually, it is not binomial. See my correct solution below.
(a) In part (a), the random variable X is the number of underweight containers in a sample of 5 containers;
so, variable X may have 6 different values 0, 1, 2, 3, 4, 5.
The probabilities are
X= 0: P(X=0) = 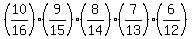 = 0.057692308 (5 not underweight containers)
choose 5 not underwait from 10 not underweight;
X= 1: P(X=1) = = 0.057692308 (5 not underweight containers)
choose 5 not underwait from 10 not underweight;
X= 1: P(X=1) = 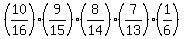 = 0.096153846 (4 not underweight; 1 underweight)
choose 4 not underwait from 10 not underweight; choose 1 underweight from 6 underweight
X= 2: P(X=2) = = 0.096153846 (4 not underweight; 1 underweight)
choose 4 not underwait from 10 not underweight; choose 1 underweight from 6 underweight
X= 2: P(X=2) = 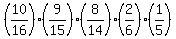 = 0.142857143 (3 not underweight; 2 underweight)
choose 3 not underwait from 10 not underweight; choose 2 underweight from 6 underweight
X= 3: P(X=3) = = 0.142857143 (3 not underweight; 2 underweight)
choose 3 not underwait from 10 not underweight; choose 2 underweight from 6 underweight
X= 3: P(X=3) = 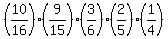 = 0.187500000 (2 not underweight; 3 underweight)
choose 2 not underwait from 10 not underweight; choose 3 underweight from 6 underweight
X= 4: P(X=4) = = 0.187500000 (2 not underweight; 3 underweight)
choose 2 not underwait from 10 not underweight; choose 3 underweight from 6 underweight
X= 4: P(X=4) = 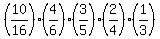 = 0.041666667 (1 not underweight; 4 underweight)
choose 1 not underwait from 10 not underweight; choose 4 underweight from 6 underweight
X= 5: P(X=5) = = 0.041666667 (1 not underweight; 4 underweight)
choose 1 not underwait from 10 not underweight; choose 4 underweight from 6 underweight
X= 5: P(X=5) = 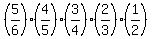 = 0.277777778 (0 not underweight; 5 underweight)
choose 5 underweight from 6 underweight
(b) Expected value is
E = 0*P(0) + 1 *P(1) + 2*P(2) + 3*P(3) + 4*(P4) + 5*P(5) =
= 0*0.057692308 + 1*0.096153846 + 2*0.142857143 + 3*0.018750000 + 4*0.041666667 + 5*277777778 = 2.499923687,
Which after rounding is about E = 2.5.
(c) See this value in (a) : P(X=2) = 0.142857143, or, after rounding, 0.1429. = 0.277777778 (0 not underweight; 5 underweight)
choose 5 underweight from 6 underweight
(b) Expected value is
E = 0*P(0) + 1 *P(1) + 2*P(2) + 3*P(3) + 4*(P4) + 5*P(5) =
= 0*0.057692308 + 1*0.096153846 + 2*0.142857143 + 3*0.018750000 + 4*0.041666667 + 5*277777778 = 2.499923687,
Which after rounding is about E = 2.5.
(c) See this value in (a) : P(X=2) = 0.142857143, or, after rounding, 0.1429.
Solved.
==================
Do not use toooo smart words like " interpret " or " comment ".
It is NOT GOOD to use them in standard school problems.
Replace them by more typical words, as I did: these more typical words
BETTER describe what the problem wants from a reader.
|
|
|