You can
put this solution on YOUR website! .
A truck can be rented from Company A for $80 a day plus $0.40 per mile.
Company B charges $50 a day plus $0.90 per mile to rent the same truck.
Find the number of miles in a day at which the rental costs for Company A and Company B are the same.
~~~~~~~~~~~~~~~~~~~
Use this equation
80 + 0.40*m = 50 + 0.90*m,
where "m" denotes miles.
The origin of this equation is so clear that I will not spend your time for explanations.
Its left and right sides speak for themselves.
From the equation,
m = 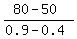 = 60.
ANSWER. 60 miles.
CHECK. 80 + 0.40*60 = 104 dollars = 50 + 0.9*60. ! correct !
= 60.
ANSWER. 60 miles.
CHECK. 80 + 0.40*60 = 104 dollars = 50 + 0.9*60. ! correct !
Solved.