|
Question 120350: i dont kno0w how to sove for substitution elimination or graphing for this problem 2x-y=1 and 3x+y=-6
Found 2 solutions by jim_thompson5910, solver91311:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
| Solved by pluggable solver: Solving a linear system of equations by subsitution |
Lets start with the given system of linear equations


Now in order to solve this system by using substitution, we need to solve (or isolate) one variable. I'm going to choose y.
Solve for y for the first equation
 Subtract Subtract  from both sides from both sides
 Divide both sides by -1. Divide both sides by -1.
Which breaks down and reduces to
 Now we've fully isolated y Now we've fully isolated y
Since y equals 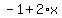 we can substitute the expression we can substitute the expression 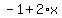 into y of the 2nd equation. This will eliminate y so we can solve for x. into y of the 2nd equation. This will eliminate y so we can solve for x.
 Replace y with Replace y with 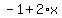 . Since this eliminates y, we can now solve for x. . Since this eliminates y, we can now solve for x.
 Distribute 1 to Distribute 1 to 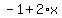
 Multiply Multiply
 Reduce any fractions Reduce any fractions
 Add Add  to both sides to both sides
 Combine the terms on the right side Combine the terms on the right side
 Now combine the terms on the left side. Now combine the terms on the left side.
 Multiply both sides by Multiply both sides by  . This will cancel out . This will cancel out  and isolate x and isolate x
So when we multiply 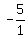 and and  (and simplify) we get (and simplify) we get
 <---------------------------------One answer <---------------------------------One answer
Now that we know that  , lets substitute that in for x to solve for y , lets substitute that in for x to solve for y
 Plug in Plug in  into the 2nd equation into the 2nd equation
 Multiply Multiply
 Add Add  to both sides to both sides
 Combine the terms on the right side Combine the terms on the right side
 Multiply both sides by Multiply both sides by  . This will cancel out 1 on the left side. . This will cancel out 1 on the left side.
 Multiply the terms on the right side Multiply the terms on the right side
 Reduce Reduce
So this is the other answer
 <---------------------------------Other answer <---------------------------------Other answer
So our solution is
 and and 
which can also look like
( , , ) )
Notice if we graph the equations (if you need help with graphing, check out this solver)


we get
 graph of graph of  (red) and (red) and  (green) (hint: you may have to solve for y to graph these) intersecting at the blue circle. (green) (hint: you may have to solve for y to graph these) intersecting at the blue circle.
and we can see that the two equations intersect at ( , , ). This verifies our answer. ). This verifies our answer.
-----------------------------------------------------------------------------------------------
Check:
Plug in ( , , ) into the system of equations ) into the system of equations
Let  and and  . Now plug those values into the equation . Now plug those values into the equation 
 Plug in Plug in  and and 
 Multiply Multiply
 Add Add
 Reduce. Since this equation is true the solution works. Reduce. Since this equation is true the solution works.
So the solution ( , , ) satisfies ) satisfies 
Let  and and  . Now plug those values into the equation . Now plug those values into the equation 
 Plug in Plug in  and and 
 Multiply Multiply
 Add Add
 Reduce. Since this equation is true the solution works. Reduce. Since this equation is true the solution works.
So the solution ( , , ) satisfies ) satisfies 
Since the solution ( , , ) satisfies the system of equations ) satisfies the system of equations


this verifies our answer.
|
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Substitution:
Eq. 1) 
Eq. 2) 
Solve equation 1 for y:



Take the expression just developed for y and substitute it into equation 2 in place of the y:


Now solve for x




 } }
Substitute this value for x into equation 1 and solve for y:




Therefore the solution set is the ordered pair (-1,-3)
Elimination:
Eq. 1) 
Eq. 2) 
Add the two equations term-by-term:
Sum: 
Solve for x

Since you have a -y in one equation and a y in the other, you can add the two equations directly to eliminate the y variable. In other problems where the coefficients are not direct additive inverses on one of the variables, you will have to multiply through one of the equations by an appropriate value to create the additive inverse situation.
To illustrate the process, I'll solve for the y variable by elimination of the x variable:


Multiply equation 1 by 3, and equation 2 by -2:


Now add the equations term by term:
Sum: 
And solve for y:

Again, the solution set is the ordered pair (-1,-3) (And I sincerely hope you aren't surprised that the two methods produce the same result. I wouldn't have been surprised necessarily if they had been different, but I would have been supremely confident that I had made an error in the performance of one or both of the methods.)
Graphing:
Select two x values for each of the lines, and then compute the corresponding y value for each selected x. This will give you two ordered pairs for each line. Plot the points and construct a straight line through each set of points. The solution will be where the two lines intersect.
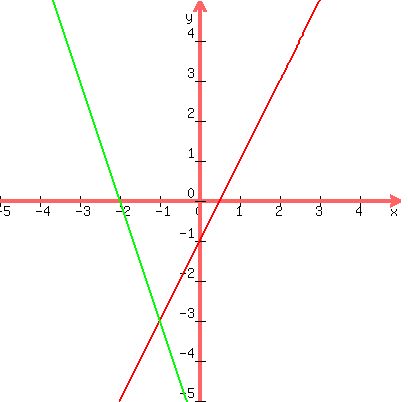
And, as we suspected, the point of intersection is (-1,-3)
Hope this helps,
John
|
|
|
| |