Question 1203483: Hi, can you please help me with this question
Find the range of x in the interval [0, 2π) for which 8 sin x + cos x > 4.
The answers are apparently 2arctan(0.2) and 2 arctan(3). I need help with my explanation. Thank you in advance.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In your words "Find the range of x in the interval [0, 2π) for which 8 sin x + cos x > 4."I think the word "range" should be "domain". Anyway:
 , , 
 Then since
Then since  , ,  or or 
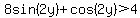 , ,  The terms on the left are trig expressions. To make the term 4 on
the right become a trig expression also, we play the clever trick
of multiplying the 4 by 1, then replacing the 1 by the familiar
Pythagorean trig identity
The terms on the left are trig expressions. To make the term 4 on
the right become a trig expression also, we play the clever trick
of multiplying the 4 by 1, then replacing the 1 by the familiar
Pythagorean trig identity  :
We use the formulas for sine and cosine of 2y: :
We use the formulas for sine and cosine of 2y:

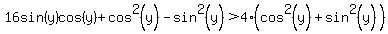


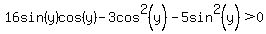


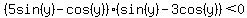 One of those factors is positive and the other is negative. So either
One of those factors is positive and the other is negative. So either
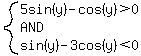 or or 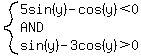 Those would involve only tan(y) if we divided through by cos(y). We could
do that as long as cos(y) is not 0. Let's make sure cos(y) is not zero.
If cos(y) were 0, then
Those would involve only tan(y) if we divided through by cos(y). We could
do that as long as cos(y) is not 0. Let's make sure cos(y) is not zero.
If cos(y) were 0, then  so let's substitute so let's substitute  in in
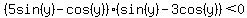
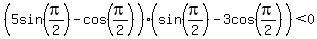
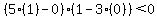
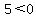 <--false!
So cos(y) can't be 0. Therefore, we can divide by it. For the first case <--false!
So cos(y) can't be 0. Therefore, we can divide by it. For the first case
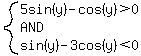
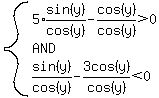
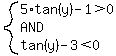
 Since tangent is a strictly increasing function,
Since tangent is a strictly increasing function,

 Now since
Now since  , ,
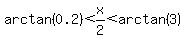
 That's the interval you were looking for. If we considered the other case
That's the interval you were looking for. If we considered the other case
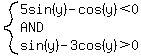 it would lead to
it would lead to
 which is a contradiction, so the domain is
which is a contradiction, so the domain is
 Edwin
Edwin
Answer by ikleyn(52879)   (Show Source): (Show Source):
|
|
|