Question 1203475: Please explain this pdf step-by-step and preferably on the pdf.
https://drive.google.com/file/d/1RDyhTvo7zrUekyy4UZ-fPXie1ygZIVVO/view?usp=drivesdk
Thank you very much
Found 4 solutions by greenestamps, Edwin McCravy, MathLover1, ikleyn:
Answer by greenestamps(13210)   (Show Source):
You can put this solution on YOUR website!
We will not, on this forum, do your complete assignment for you; the rules of the forum say one problem per post. And I doubt that we have the capability of providing our answers on the link you provided.
I will explain the first problem for you. If you want help with the others, you need to post them individually -- entering each question using your keyboard instead of giving a link.
First problem then....
To understand binomial expansion, view the expression 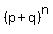 as the product of n factors of  .
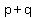In multiplying n factors of 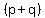 , each partial product is obtained by choosing either the p or the q from each of the n factors. That means that in each partial product the sum of the exponents on p and q has to be n.
To get a partial product that includes the expression p^n, you need to pick the p from each of the n factors.
To get a partial product that includes p^5, you need to pick the p from 5 of the n factors and the q from the other (n-5) factors.
Consider then a table of the term number, the exponents on p and q, and the coefficient of the term in the full expansion of .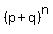
term # exponent on p exponent on q coefficient
----------------------------------------------------
1 n 0 C(n,n) = C(n,0) [you need to choose "p" in all n factors and "q" in none of them]
2 n-1 1 C(n,n-1) = C(n,1) [you need to choose "p" in (n-1) of the n factors and "q" in 1 of them]
3 n-2 2 C(n,n-2) = C(n,2) [you need to choose "p" in (n-2) of the n factors and "q" in 2 of them]
...
n 1 n-1 C(n,1) [you need to choose "p" in 1 of the n factors and "q" in (n-1) of them]
n+1 0 n C(n,0) [you need to choose "p" in 0 of the n factors and "q" in all n of them]
Looking at the patterns in the table, we see that the k-th term contains expressions of
(1) 
(2)  =
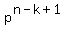
(3) 
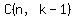
From that pattern we can see that the first term is p^n and the last term is q^n, so the first of the possible answer choices is true and the next three are not.
And from the pattern we can see that for the k-th = 4th term, k-1 is 4-1 = 3, so the 5th possible answer choice is true and the last one is not.
Answer by Edwin McCravy(20064)  (Show Source):
Answer by MathLover1(20850)  (Show Source):
Answer by ikleyn(52897)  (Show Source):
You can put this solution on YOUR website! .
It is fantastically good business idea - in order for the volunteer tutors
make the answer cards for you, for free, immediately in pdf-format.
It looks like you are the first at this forum with such an advanced idea !
Hurry to patent the idea, before others get ahead of you !
Next time, as you get other similar brilliant business idea,
please report to us immediately !
|
|
|
