|
Question 1203435: https://brainly.com/question/36509846
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52915)   (Show Source):
You can put this solution on YOUR website! .
Solve the equation y^2=81
~~~~~~~~~~~~~~~~~~
Solution 1
y^2 = 81 implies y = +/- 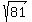 = +/- 9 (taking square roots from both sides).
ANSWER. There are two solutions: y= 9 and y= -9.
Solution 2
y^2 = 81
y^2 - 81 = 0
Factor left side
(y-9)*(y+9) = 0.
There are two solutions y= 9 and y= -9. ANSWER
Solved in two ways, for your better understanding.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
The tutor @ikleyn has shown two great approaches.
I'll show two more methods.
Instead of y, I'll use x.
The task is to solve x^2 = 81 which is the same as x^2-81 = 0
Further we can write
1x^2 + 0x + (-81) = 0
Compare that to the template
ax^2 + bx + c = 0
to find that:
a = 1
b = 0
c = -81
Those values are plugged into the quadratic formula.
 or 
 or 
 or 
While this method takes a bit more work, I think it's still handy to know multiple approaches.
----------------------------------------
Another approach is to graph y = x^2 - 81 using a tool like Desmos or GeoGebra.
This produces a parabola that opens upward. The parabola crosses the x axis at x = 9 and x = -9, which are the two solutions to x^2 = 81.
Window: xmin = -10, xmax = 10, ymin = -100, ymax = 100
Link to the interactive Desmos graph
https://www.desmos.com/calculator/ewdbmqwf2c
Therefore, the two solutions to y^2 = 81 are y = 9 or y = -9
As a quick check,
y^2 = 81
9^2 = 81
9*9 = 81
81 = 81
and also
y^2 = 81
(-9)^2 = 81
(-9)*(-9) = 81
81 = 81
When squaring the negative, the two negatives cancel out to get a positive.
In other words: negative times negative = positive
We get the same thing on both sides (81), so we have confirmed the answers are correct.
|
|
|
| |
