SOLUTION: The point $(x,y)$ in the coordinate has a distance of $6$ units from the $x$-axis, a distance of $15$ units from the point $(5,7)$, and a distance of $\sqrt{n}$ from the origin. I

Click here to see ALL problems on Percentage-and-ratio-word-problems

Question 1203373: The point $(x,y)$ in the coordinate has a distance of $6$ units from the $x$-axis, a distance of $15$ units from the point $(5,7)$, and a distance of $\sqrt{n}$ from the origin. If both $x$ and $y$ are negative, what is $n$?
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200) (Show Source):
You can put this solution on YOUR website!

The point (x,y) is in quadrant III, because x and y are both negative.

Because the point is 6 units from the x-axis, y is -6. So the point is (x,-6).

The distance from (x,-6) to (5,7) is 15. The difference in the y coordinates is 13, the distance is 15; find the difference in the x coordinates.

.

The point (x,y) is 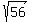units left of x=5, so the point is (5-sqrt(56)),-6)

The point is 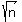units from the origin:

= 42.167 to 3 decimal places.

ANSWER: (approximately) 42.167

Answer by MathLover1(20850) (Show Source):
You can put this solution on YOUR website!

given:
the distance between (, ) and the -axis is units.
The nearest point to (,) in the -axis is the point (, ) so we have:

can be or

So we know that and are negative, our point will be in Q III.

so, and now we can write our point as (, )

the distance between our point and (,) is units:

or

And we know that the distance from the origin, (, ) is :

(approximately)