|
Question 1203353: A cone has a volume of 60 cubic cm. Determine the volume of a cylinder with the same circular base as the cone, but the height is 10 times taller.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 1800 cubic cm
================================================================
Here's one approach
A second approach is talked about in the next section.
r = radius of the cone = radius of the cylinder
We know this because both 3D objects have the same circular base.
h = height of the cone
10h = height of the cylinder
volume of a cone = (1/3)*pi*(radius)^2*(height)
Vcone = (1/3)*pi*r^2*h
volume of a cylinder = pi*(radius)^2*(height)
Vcylinder = pi*r^2*(10h)
We see that "pi*r^2" is involved with both formulas. Let's replace that with B to represent the area of the base.
Vcone = (1/3)*pi*r^2*h
Vcone = (1/3)*Bh
and
Vcylinder = pi*r^2*(10h)
Vcylinder = B(10h)
Vcylinder = 10Bh
Both now involve Bh
Let's isolate Bh in the 1st formula
Vcone = (1/3)*Bh
Bh = 3*Vcone
Then we can use substitution
Vcylinder = 10Bh
Vcylinder = 10*(3*Vcone)
Vcylinder = 10*(3*60)
Vcylinder = 1800 cubic cm is the final answer
-------------------------------------------------------
Another approach
Let's consider making the cone 10 times taller.
We'll keep the circular base the same.
This will mean,
new cone volume = 10*(old cone volume)
new cone volume = 10*(60)
new cone volume = 600 cubic cm
Why does this work?
Well consider a rectangular prism of length, height, width of L,W,H
We'll scale H to 10H to make it 10 times taller. Keep everything else the same.
old volume = LWH
new volume = LW(10H) = 10LWH = 10*(old volume)
This idea can be applied to the cone because we can break the cone into very small cubic blocks.
Then recall the connection between a cylinder and a cone.
cone volume = (1/3)*(cylinder volume)
which rearranges to
cylinder volume = 3*(cone volume)
So we can fit 3 cones in a cylinder when these two conditions are true- The circular base areas are the same. This is equivalent to saying "The radii are the same" (or "the diameters are the same").
- The height of the cone and cylinder are the same.
So you can probably see why I scaled the cone up so its height is 10 times taller.
From here we then write:
cylinder volume = 3*(new cone volume)
cylinder volume = 3*(600)
cylinder volume = 1800 cubic cm
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When professional Math writers formulate Math problems in English,
they NEVER use the form " 10 times taller ", because such form is ambiguous in English.
The standard form to use in Math problems in English for such situations
is " 10 times as tall as . . . ".
The strict formal meaning of the form " 10 times taller than . . . "
in English is " 11 times as tall as . . . ".
You will be very surprised, but it is so, to great distinction from other languages,
as well as from your native language.
To learn more, read from this link
https://english.stackexchange.com/questions/221323/has-the-illogical-three-times-bigger-replaced-three-times-as-big-in-common-u
This error that you make in your post is a standard/typical mistake for newcomers:
they ALL do this mistake, until somebody will disclose them the truth.
////////////////
As for the solution, below it is presented in short form.
If "r" is the radius of the base of a cone and "h" is the cone's height,
then the volume of a cone is
 = =  .
From the problem, we are given that .
From the problem, we are given that
 = =  = 60 cm^3.
It implies that = 60 cm^3.
It implies that
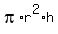 = 3*60 = 180 cm^3.
This formula says that the volume of a cylinder with the same base and the same height is 180 cm^3.
But since our cylinder is 10 times as tall as the cone, we should take 180 cm^3 ten times, which gives us the
ANSWER. The volume of the cylinder under the problem's question is 1800 cm^3. = 3*60 = 180 cm^3.
This formula says that the volume of a cylinder with the same base and the same height is 180 cm^3.
But since our cylinder is 10 times as tall as the cone, we should take 180 cm^3 ten times, which gives us the
ANSWER. The volume of the cylinder under the problem's question is 1800 cm^3.
Solved.
|
|
|
| |