Question 1203351: On a travel website, 58 hotels are rated 5 stars, 120 hotels are rated 4 stars, 135 hotels are rated 3 stars, 88 hotels are rated 2 stars, and 46 hotels are rated 1 star. What is the average hotel rating?
Found 3 solutions by MathLover1, math_tutor2020, ikleyn:
Answer by MathLover1(20850)   (Show Source):
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
I recommend a spreadsheet for this problem.
x = score = star rating
f = frequency
Make the following frequency table
Form a third column where we multiply each x and f value.
| x | f | x*f | | 5 | 58 | 290 | | 4 | 120 | 480 | | 3 | 135 | 405 | | 2 | 88 | 176 | | 1 | 46 | 46 | | Total | 447 | 1397 |
At the bottom of columns 2 and 3 are the sums of those respective columns.
Divide the sum of the xf values over the sum of the frequencies.
1397/447 = 3.12527964205817
The average hotel rating is about 3.125
------------------------------------------
The much longer method, and the method I strongly do NOT recommend, is to write 58 copies of "5", 120 copies of "4", 135 copies of "3", and so on until you have a massive set of values (447 values in total).
Then compute the mean by adding up those values to get a sum of 1397.
Divide that sum over the sample size 447 to get the answer mentioned earlier.
Thankfully the first method involving a frequency chart helps give a nice shortcut.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
As this problem is given in the post, it is very elementary level,
typical for students who start learning a conception of "Average".
It is approximately 6th - 7th grade level of middle school,
when a typical student is unfamiliar yet with computer tools like Excel.
At this level, it is absolutely admittable/allowable to use a standard calculator
and to use the formula for a weighted average
average =  =  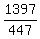= 3 (rounded).
I would say that this method solving this problem is the most expected way.
At this level, the major goal of the solution is to learn the formula,
to understand its meaning and to know how it works.
Which tool to use - is just the secondary question.
Notice that in my solution I rounded my answer to the closest integer number,
since the rating of hotels are usually expressed in integer values.
The fact that the rating of a hotel is usually an integer number is not a necessary requirement
to round the average to an integer number. It is simply an argument "pro".
Nevertheless, you may round to one decimal, too. It will show you to which integer the average value
is closer - to a "3" or to a "4", which still makes sense.
But rounding to two or more decimals just makes no any reasonable sense - at least, I do not see such a reason.
Next, many students learn the conception of Average in colleges or universities repeatedly
in more older age, when they are just familiar with computers and tools like Excel.
Then it is totally acceptable to use Excel on your computer and solve this problem
as the tutor @Math_tutor2020 does recommend in his post.
----------------------
To see many other similar (and different) solved problems on Average, look into the lessons
- Solved problems on average scores
- Solved problems on average age
- Miscellaneous problems on average values
- Math circle level problem on average
- Entertainment problems on average
in this site.
Learn the subject from there, once and for all.
|
|
|
