|
Question 1203333: Find the range of
f(x) =sqrt(x²-2) + sqrt((1+x)/(2+x²)) - (8+x²)/(x² -4x-1)
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!




Analyze the three parts separately, considering the domain for each.
p(x) is always positive and is undefined for 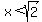 . So we know the domain of f(x) is restricted to . So we know the domain of f(x) is restricted to  . .
For large positive or large negative x, p(x) is very close to 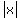 . .
q(x) is always positive; and since the degree of the denominator is greater than the degree of the numerator, the value of q(x) will never be large. Graphing q(x) alone shows its maximum value is less than 1. So q(x) will not be a determining factor in finding the range of f(x).
r(x) is undefined at the roots of the quadratic denominator. The positive root is 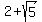 ; we know we aren't concerned with the negative root, since the domain of f(x) includes no negative numbers. ; we know we aren't concerned with the negative root, since the domain of f(x) includes no negative numbers.
The numerator of r(x) is always positive. The denominator graphs as an upward-opening parabola, so it is negative for x just less than 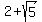 and positive for x just greater than and positive for x just greater than 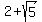 ; with the negative sign on r(x), that means r(x) is arbitrarily large for x just less than ; with the negative sign on r(x), that means r(x) is arbitrarily large for x just less than 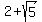 and arbitrarily small for x just greater than and arbitrarily small for x just greater than 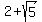 . .
For large x, r(x) is very close to -1.
So f(x) is...
(1) undefined for 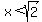 ; ;
(2) dominated by r(x) for x close to 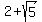 (about 4.236), having arbitrarily large positive values to the left of the root and arbitrarily large negative value to the right; and (about 4.236), having arbitrarily large positive values to the left of the root and arbitrarily large negative value to the right; and
(3) dominated by p(x) for large x, with f(x) being approximated by p(x)-1.
Since r(x) is arbitrarily large negative and arbitrarily large positive in the vicinity of 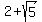 , that means that the range of f(x) is all real numbers. , that means that the range of f(x) is all real numbers.
ANSWER: The range of f(x) is all real numbers
A graph confirms that; and it also shows that f(x) (red) is approximated by p(x) (green) for large x.

|
|
|
| |