Question 1203324: Eighteen points are equally spaced on a circle, from which you will choose a certain number at random. How many do you need to choose to guarantee that you will have the four corners of at least one rectangle?
Found 3 solutions by ikleyn, greenestamps, math_helper:
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Eighteen points are equally spaced on a circle, from which you will choose a certain number at random.
How many do you need to choose to guarantee that you will have the four corners of at least one rectangle?
~~~~~~~~~~~~~~~~~~~~~~
Let the points on the circle are numbered consequently from 1 to 18, inclusive.
Let call them  , ,  , , 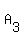 , . . . , , . . . , 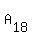 .
Notice that if a rectangle is inscribed in a circle, then its diagonals are DIAMETERS
of the circle. So, the opposite verices of the rectangle are the opposite points on the circle.
Thus, diagonals of our rectangle connect opposite points on the circle.
Of 18 points .
Notice that if a rectangle is inscribed in a circle, then its diagonals are DIAMETERS
of the circle. So, the opposite verices of the rectangle are the opposite points on the circle.
Thus, diagonals of our rectangle connect opposite points on the circle.
Of 18 points  , ,  , , 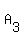 , . . . , , . . . , 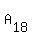 , we have 9 pairs with opposite points
( , we have 9 pairs with opposite points
( , ,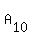 ), ( ), ( , , ), . . . , ( ), . . . , (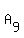 , ,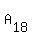 ).
Now my statement is that the ANSWER to the problem's question is 11 points of 18.
Indeed, among these 11 points, there is at least one pair of opposite points.
Removing this pair, you have remaining 16 points and 11-2 = 9 selected points.
Among these 9 selected points, there is at least one another pair of opposite points.
So, 11 points are ENOUGH, even in the WORST CASE.
From the other side, taking 10 points ).
Now my statement is that the ANSWER to the problem's question is 11 points of 18.
Indeed, among these 11 points, there is at least one pair of opposite points.
Removing this pair, you have remaining 16 points and 11-2 = 9 selected points.
Among these 9 selected points, there is at least one another pair of opposite points.
So, 11 points are ENOUGH, even in the WORST CASE.
From the other side, taking 10 points  , ,  , , 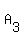 , . . . , , . . . , 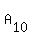 , it is clear, that
among them, there is ONLY ONE pair ( , it is clear, that
among them, there is ONLY ONE pair ( , ,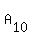 ) of opposite points to make a diameter/(=a diagonal),
and there are NO points to make another pair/(=another diagonal).
ANSWER. 11 points are needed to choose to GUARANTEE
that you will have the four corners of at least one rectangle. ) of opposite points to make a diameter/(=a diagonal),
and there are NO points to make another pair/(=another diagonal).
ANSWER. 11 points are needed to choose to GUARANTEE
that you will have the four corners of at least one rectangle.
Solved.
--------------------
I want to make three POST-solution notes.
(1) This problem is a TWIN to another popular classic problem about 18 socks in a drawer.
These 18 socks are of 9 different colors, are separated and lie in disorder.
How many socks should a person take from a drawer without looking (without seeing)
to guarantee that among selected socks there are at least two proper pairs?
(2) The condition that the points are uniformly distributed on the circle DOES NOT MATTER
in this problem, and I did not used it in my solution. What really does matter is that
these 18 points are, actually, 9 pair of opposite points.
The words "uniformly distributed" are used to disguise this fact and to distract
attention of a reader from using this conception of opposite points.
(3) Interesting, that in the Internet, there is a solution to this problem,
generated by the artificial intelligence chatGPT
https://www.quora.com/Eighteen-points-are-equally-spaced-on-a-circle-from-which-a-number-are-chosen-at-random-How-many-must-you-choose-to-guarantee-that-you-will-have-to-the-four-corners-of-at-least-one-rectangle
+--------------------------------------------------+
| AND THIS SOLUTION IS INCORRECT ( ! ! ! ) |
+--------------------------------------------------+
It confirms my idea that so called AI in its contemporary status
is simply big (VERY BIG, huge) GARBAGE BIN.
Regarding this so called AI in Math education, it is simply a way
to make money without taking any responsibility for a correctness
of solutions and quality of final product.
///////////////////
To see many other similar (and different) solved problems, look into the lesson
- In the worst case
in this site.
Learn from good sources ( ! ) Then everything will be OK.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If 4 points on the circle determine a rectangle, then there are 2 of those points on each half of the circle.
So the worst case, if you are trying to get a rectangle with the points you choose, is to first pick all 9 points on one half of the circle. Then any 2 points on the other half of the circle will determine a rectangle.
ANSWER: 9+2 = 11
Note this solution is easier to see by drawing sketches to consider cases with smaller even numbers of point on the circle.
6 points: choose the 3 on one side of the circle; any one 4th point still does not determine a rectangle, but then any 5th point does. 3+2 = 5
8 points: choose the 4 on one side of the circle; any one 5th point still does not determine a rectangle, but then any 6th point does. 4+2 = 6
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Tutor ikleyn: That is very interesting about ChatGPT! Makes one wonder: how many people will just take the ChatGPT answer without questioning it!
|
|
|