Question 1203310: if the volume of a hexagonal pyramid is 750 units 3 and the base and the height being 5 units and 10 units respectively, what is the length of apothem of the pyramid?
Found 3 solutions by math_tutor2020, ikleyn, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
Answer by ikleyn(52784)  (Show Source):
You can put this solution on YOUR website! .
if the volume of a hexagonal pyramid is 750 units 3 and the base and the height being
5 units and 10 units respectively, what is the length of apothem of the pyramid?
~~~~~~~~~~~~~~~~~~~
As the problem is worded, printed, posted and presented in this parcel,
it is SELF-CONTRADICTORY and can not be solved.
Below I explain it in a comprehensive way, with all details.
The term "apothem" is used in Geometry in combination with the conception of a regular polygon, ONLY.
So, I am forced to assume that the base is a regular hexagon - I have NO other choice.
Then it is clear that three longest diagonals divide the base of the hexagonal regular pyramid
in 6 congruent equilateral triangles with the side length of a=5 units each.
Hence, the area of each such a triangle is
area of a triangle = 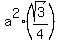 =  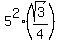square units.
The area of the hexagonal base is 6 times this value
area of the base = 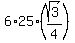 =  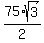= 64.95191 square units.
The volume of the pyramid is then
V = 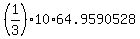 = 216.530176 cubic units,
which is  from the given value of 750 cubic units.
Thus the given data as the input is INCONSISTENT.
The problem CAN NOT be solved in this formulation.
Also, if the length of a base side is given, then the apothem
can be found in one single and simple line.
Neither volume of a pyramid, nor its height are needed for such calculations.
By creating this nonsense, the problem's composer deserves to be ticketed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
To start with, the problem is deficient in not stating that the base of the pyramid is a REGULAR hexagon.
Next, it is not clear what "base... being 5 units" means.
Finally, the problem is overprescribed when the "base", volume, and height of the pyramid are all given and are not consistent.
The only possible way to solve the problem is to ignore one of the given pieces of information. Since it is not clear what a "base of 5" means, I will ignore that.
So my GUESS as to the correct information in the problem is a pyramid with a regular hexagonal base, a height of 10, and a volume of 750. Then....
ASSUMING the hexagonal base is regular, each of the equilateral triangles that comprise the base have area 225/6 = 37.5. In terms of the length a of the apothem, that area (one-half base, times height) is  . So
In exact form, the length of the apothem (with all the assumptions that have been made) is
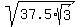
That's 8.06 to 2 decimal places.
Again, however, note that the presentation of the problem is exceedingly poor....
|
|
|
