|
Question 1203277: James used 1/4 of his money to buy 3 pencil cases and 7 key chains. The cost of each pencil case is 3 times the cost of each key chain. He bought some more key chains with 5/6 of his remaining money. He spent $30.40 more on all the key chains than on all the pencil cases. How much was the cost of one key chain?
Found 3 solutions by ikleyn, math_tutor2020, MathTherapy:
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(1) James used 1/4 of his money to buy 3 pencil cases and 7 key chains.
(2) The cost of each pencil case is 3 times the cost of each key chain.
(3) He bought some more key chains with 5/6 of his remaining money.
(4) He spent $30.40 more on all the key chains than on all the pencil cases.
How much was the cost of one key chain?
~~~~~~~~~~~~~~~~~
I numbered the problem' statements for easy references.
Let x be the price of one key chain, in dollars (the unknown value under the problem's question).
Then the price for one pencil case is 3x dollars, according to the problem's statement (2).
The cost of the first purchase (3 pencil cases and 7 key chains) was 3(3x) + 7x = 9x + 7x = 16x.
This cost was 1/4 of his money originally - hence, the original amount of money was 4*(16x) = 64x.
After his first purchase, the remaining money was 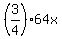 = 48x.
James bought additional key chains for = 48x.
James bought additional key chains for 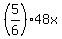 = 40x dollars.
For key chains, he spent, in all, 7x + 40 = 47x dollars.
For all pencil cases, he spent 3*(3x) = 9x dollars.
The difference is 47x - 9x = 38x.
From (4), we have this equation for the difference
38x = 30.40 dollars.
Hence, x = = 40x dollars.
For key chains, he spent, in all, 7x + 40 = 47x dollars.
For all pencil cases, he spent 3*(3x) = 9x dollars.
The difference is 47x - 9x = 38x.
From (4), we have this equation for the difference
38x = 30.40 dollars.
Hence, x = 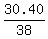 = 0.80 dollars.
ANSWER. The cost of one key chain is $0.80. = 0.80 dollars.
ANSWER. The cost of one key chain is $0.80.
Solved.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x = cost of 1 key chain
3x = cost of 1 pencil case
costs are in dollars
x > 0
3(3x) = 9x = cost of 3 pencil cases
7x = cost of 7 key chains
9x+7x = 16x = cost of 3 pencil cases and 7 key chains
James used 1/4 of his money to buy 3 pencil cases and 7 key chains.
He used 1/4 of his money to spend 16x dollars.
(1/4)*(his starting amount of money) = amount spent
(1/4)*(his starting amount of money) = 16x dollars
his starting amount of money = 4*16x dollars
his starting amount of money = 64x dollars
James started with 64x dollars.
3/4 of 64x = 48x dollars left over
Or we could say: 64x - 16x = 48x
Then,
5/6 of 48x = 40x dollars spent on more key chains
James spent 7x dollars on 7 key chains, and then an additional 40x dollars on some more key chains.
That's a total of 7x+40x = 47x dollars spent on all of the key chains.
Now we'll use this fact: "He spent $30.40 more on all the key chains than on all the pencil cases."
Amount spent on key chains = Amount spent on pencil cases + 30.40
47x = 9x + 30.40
47x-9x = 30.40
38x = 30.40
x = 30.40/38
x = 0.80
One key chain costs $0.80, aka 80 cents
3x = 3*$0.80 = $2.40 is the cost of 1 pencil case.
-------------------------------------------
Check:
1 pencil case = $2.40
3 pencil cases = 3*$2.40 = $7.20
1 key chain = $0.80
7 key chains = 7*$0.80 = $5.60
3 pencil cases and 7 key chains = $7.20 + $5.60 = $12.80
He spent 1/4 of his money and spent $12.80
Therefore he started with 4*12.80 = $51.20
3/4 of which is what he has left: (3/4)*$51.20 = $38.40
Or we could say 51.20 - 12.80 = 38.40
After buying that first batch of pencil cases and key chains, he has $38.40 left over.
5/6 of $38.40 = $32 is spent on additional key chains
Each key chain is $0.80, so he must have bought 32/0.80 = 40 additional key chains.
He bought a total of 7+40 = 47 key chains
47*0.80 = $37.60 was spent on key chains
$7.20 was spent on pencil cases
37.60-7.20 = 30.40 is the difference in what was spent on each item type.
We have confirmed the answer.
----------------------------------------------------------------
----------------------------------------------------------------
Answer: One key chain costs $0.80 (aka 80 cents)
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website!
James used 1/4 of his money to buy 3 pencil cases and 7 key chains. The cost of each pencil case is 3 times the cost of each key chain. He bought some more key chains with 5/6 of his remaining money. He spent $30.40 more on all the key chains than on all the pencil cases. How much was the cost of one key chain?
Let original amount he had, and cost of each key chain, be A and K, respectively
He used  of his money of his money 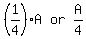 to buy 3 pencil cases and 7 key chains, leaving to buy 3 pencil cases and 7 key chains, leaving 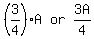 Therefore, cost of the 7 key chains (K) = 7K, and the cost of the 3 pencil cases =
Therefore, cost of the 7 key chains (K) = 7K, and the cost of the 3 pencil cases = 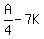 So, cost of 1 pencil case =
So, cost of 1 pencil case = 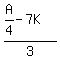 Since the cost of each pencil case is 3 times the cost of each key chain, we get:
Since the cost of each pencil case is 3 times the cost of each key chain, we get:  A = 36K + 28K
A = 64K --- eq (i)
Since he then used
A = 36K + 28K
A = 64K --- eq (i)
Since he then used  of remaining money to buy more key chains, he used of remaining money to buy more key chains, he used 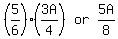 to buy more key chains.
Amount spent on key chains: to buy more key chains.
Amount spent on key chains: 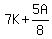 Amount spent on pencil cases:
Amount spent on pencil cases: 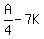 He spent $30.40 more on ALL key chains than on pencil cases, and so:
He spent $30.40 more on ALL key chains than on pencil cases, and so:  112K + 5A - 2A = 243.2 -- Multiplying by LCD, 8
112K + 3A = 243.2 -- eq (ii)
112K + 3(64K) = 243.2 -- Substituting 64K for A in eq (ii)
112K + 192K = 243.2
304K = 243.2
Cost of each key chain, or
112K + 5A - 2A = 243.2 -- Multiplying by LCD, 8
112K + 3A = 243.2 -- eq (ii)
112K + 3(64K) = 243.2 -- Substituting 64K for A in eq (ii)
112K + 192K = 243.2
304K = 243.2
Cost of each key chain, or 
|
|
|
| |