Question 1203260: Alonzo, Bob, and Casper work bussing tables at a restaurant. Alonzo has a 60% chance, Bob has a 10% chance, and Casper has a 30% chance of bussing tables in the middle area of the restaurant. If Alonzo is bussing tables, he has a 6% chance of breaking a dish. If Bob is bussing tables, he has a 2% chance of breaking a dish. Finally, if Casper is bussing tables, he has a 4% chance of breaking a dish. If there is a broken dish in the middle of the restaurant, what is the probability it was broken by Casper?
Multiple Choice
0.012
0.040
0.240
0.720
Found 3 solutions by math_tutor2020, ikleyn, Edwin McCravy:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: Choice C) 0.240
===============================================================================================
Explanation
There are at least two methods we can use.
Method 1
A = Alonzo buses tables in the middle area
B = Bob buses tables in the middle area
C = Casper buses tables in the middle area
D = Dish is broken in the middle area
From the second sentence of the instructions, we are given these 3 pieces of info:
P(A) = 0.60
P(B) = 0.10
P(C) = 0.30
The next 3 sentences offer these additional 3 pieces of info:
P(D given A) = 0.06
P(D given B) = 0.02
P(D given C) = 0.04
Goal: Compute P(C given D)
In other words, we want to find P(C) when we know event D has occurred.
Use Bayes' Theorem
P(C given D) = P(D given C)*P(C)/P(D)
We already have the values of P(D given C) and P(C)
We'll need P(D)
Use the Law of Total Probability
P(D) = P(D and A) + P(D and B) + P(D and C)
P(D) = P(D given A)*P(A) + P(D given B)*P(B) + P(D given C)*P(C)
P(D) = 0.06*0.60 + 0.02*0.10 + 0.04*0.30
P(D) = 0.05
We have enough info to compute the following
P(C given D) = P(D given C)*P(C)/P(D)
P(C given D) = 0.04*0.30/0.05
P(C given D) = 0.012/0.05
P(C given D) = 12/50
P(C given D) = 6/25
P(C given D) = 0.240
This is why the final answer is choice C
-------------------------------------------------------
Method 2
Let's say that there are 1000 instances of a single dish being bused.
Alonzo handles 60% of them, Bob does 10%, Casper does the remaining 30%
60% of 1000 = 0.60*1000 = 600
10% of 1000 = 0.10*1000 = 100
30% of 1000 = 0.30*1000 = 300
So,
Alonzo buses 600 times
Bob buses 100 times
Casper buses 300 times
Alonzo breaks a dish 6% of the time
6% of 600 = 0.06*600 = 36
If Alonzo buses 600 times then we expect him to break around 36 dishes.
Bob breaks a dish 2% of the time
2% of 100 = 0.02*100 = 2
If Bob buses 100 times then we expect him to break around 2 dishes.
Casper breaks a dish 4% of the time
4% of 300 = 0.04*300 = 12
If Casper buses 300 times then we expect him to break around 12 dishes.
An total estimate of 36+2+12 = 50 dishes have been broken.
P(D) = probability of a broken dish
P(D) = (50 dishes broken)/(1000 dishes total)
P(D) = 50/1000
P(D) = 0.05
This was calculated earlier in the previous section.
Of those 50 broken dishes, Casper is estimated to break 12 of them.
12/50 = 0.240
If we encounter a broken dish, then there's a 24% chance that Casper did it.
Answer by ikleyn(52809)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Alonzo, Bob, and Casper work bussing tables at a restaurant. Alonzo has a 60% chance, Bob has a 10% chance,
and Casper has a 30% chance of bussing tables in the middle area of the restaurant.
If Alonzo is bussing tables, he has a 6% chance of breaking a dish.
If Bob is bussing tables, he has a 2% chance of breaking a dish.
Finally, if Casper is bussing tables, he has a 4% chance of breaking a dish.
If there is a broken dish in the middle of the restaurant, what is the probability it was broken by Casper?
~~~~~~~~~~~~~~~~~~~
If you got such problem, hence, you just have some preliminary basic knowledge in Probability.
As you read the problem, it should be clear to you that it is about conditional probability.
So, this probability is the fraction, whose denominator is the probability of the event
"there is a broken dish in the middle of the restaurant", and the numerator is the probability
"the dish was broken by Casper".
The probability "there is a broken dish in the middle of the restaurant" is this expression
(Alonzo) (Bob) (Casper)
0.6*0.06 + 0.1*0.02 + 0.3*0.04. <<<---=== sum of possible contributions of each participant
We take the sum of partial probabilities, because the relevant events are disjoint.
The probability "the dish was broken by Casper" is this expression
0.3*0.04.
Therefore, the final probability under the problem's question is
P = 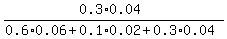 = use your calculator = 0.240.
ANSWER. P = 0.240. = use your calculator = 0.240.
ANSWER. P = 0.240.
Solved.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Maybe the student could see it better if we explained it in terms of "AND usually
means MULITIPLY" and "OR usually means ADD". The desired probability is:
P("C bussed" AND "C broke dish")
--------------------------------------------------------------------------------------------------------
P[("A bussed" AND "A broke dish") OR ("B bussed" AND "B broke dish") OR ("C bussed" AND "C broke dish")]
which means that we perform these operations:
P("C bussed") x P(C broke dish")
---------------------------------------------------------------------------------------------------------
P("A bussed") x P("A broke dish") + P("B bussed") x P("B broke dish") + P("C bussed") x P("C broke dish")
0.3 x 0.04
------------------------------------
0.6 x 0.06 + 0.1 x 0.02 + 0.3 x 0.04
which comes out to be 0.24.
Edwin
|
|
|