Question 1203198: Hi. This is a base arithmetic question.
"Is there any base b such that 3443 base b is a prime number? If yes, provide an example. If not, explain why not."
I've been stuck for a while. Any help on how to prove this would be appreciated. Thank you so much!
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
This question in the post is nonsensical.
The fact, if the number 3443 is a prime number or not,
does not depend on any "base".
3443 = 11*313, so 3443 is a composite, not a prime number.
A collection of words in the post is "soup of words with no sense" (not edible).
If one wants the meaning of the problem be understandable,
then its formulation (its wording) should be different.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
3443 = 11 * 313
This shows 3443 is not prime. It is composite.
It doesn't matter which base you are working with because we can convert between any two bases.
A prime number in one base, is a prime number in any base.
Some examples:
The subscript represents which base we're working in
For instance 
Further Reading:
https://math.stackexchange.com/questions/3999/is-a-prime-number-still-a-prime-when-in-a-different-base
and
http://web.archive.org/web/20190714164706/http://mathforum.org/library/drmath/view/55880.html
Useful calculator
https://www.rapidtables.com/convert/number/base-converter.html
---------------------------------
Another approach
Use the rational root theorem to determine that b = -1 is a root of 
Therefore, (b+1) is a factor
Use polynomial long division, or the shortcut synthetic division, to find that 
That rearranges to 
For  to be prime, one of the factors must be 1.
If b+1 = 1, then b = 0. But we can't have base 0.
If 3b^2+b+3 = 1, then it leads to two nonreal complex roots.
The base cannot be complex as only positive integers are allowed
Specifically from the set {5,6,7,8,9,...} so we can form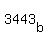 
We conclude that neither factor (b+1) nor (3b^2+b+3) can be 1.
Therefore, is never prime. It is always composite.
|
|
|
