Question 1203180: Dear maths genii.
I have a query involving direct variation.
A question states: ‘The surface area of a sphere, SAmm2, varies directly as the square of its diameter, dmm. If the surface area is doubled, by what ratio must the diameter be altered?’
So SA∝d2
Let us imagine that we have a sphere and we are told that the surface area is 100cm2.
The surface area of a sphere is 4Πr2.
4Πr2 = 100
r2 = 100/4Π
r2 = 7.96
r = 2.82cm, d = 5.64cm and d2 = 31.81cm
SA∝d2
therefore 100 = kd2
therefore 100 = k(31.81)
therefore k = 3.18
If we then double the surface area of the sphere to 200cm2,
200 = 4Πr2
r2 = 200/4Π
r2 = 15.92
r = 3.99, d = 7.98 and d2 = 63.66
Therefore 200 = k(63.66) and k = 3.14 again.
Thus given any diameter I can work out the surface area of a sphere, knowing k. What does ‘…by what ratio must the diameter be altered?’ mean and why do I have to do anything other than what I have done already?
Marcus Clayson
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! ----------
I have a query involving direct variation.
A question states: ‘The surface area of a sphere, SAmm2, varies directly as the square of its diameter, dmm. If the surface area is doubled, by what ratio must the diameter be altered?’
----------
Written very strangely. Difficult symbolism used.
Could you say it like this?
===
‘The surface area of a sphere, s, varies directly as the square of its diameter, d. If the surface area is doubled, by what ratio must the diameter be altered?’
===
Be much easier to read.
.
.
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problem says A = k*d^2 (surface area of a sphere SA varies directly as the square of its diameter, d).
Then it asks "If the surface area is doubled, by what ratio must the diameter be altered?".
So we write
 = = 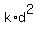 , (1) , (1)
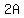 = = 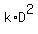 (2)
and divide equation (2) by equation (1). We get then
2 = (2)
and divide equation (2) by equation (1). We get then
2 =  ,
which implies ,
which implies
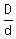 = =  = 1.414213562...
In wording form, it means that if the surface area of a sphere is doubled, then the ratio
of the new diameter to the original diameter is = 1.414213562...
In wording form, it means that if the surface area of a sphere is doubled, then the ratio
of the new diameter to the original diameter is 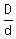 = =  = 1.414213562...,
which gives the answer to the problem's question. = 1.414213562...,
which gives the answer to the problem's question.
--------------
Solved, with complete explanations.
This solution (or something very similar) is what they do expect to get from you.
==================
Regarding your solution, notice that
- you do unnecessary calculations;
- you do not get a general answer;
- you use centimeters and square centimeters instead of millimeters and square millimeters.
So, you play some your own game, but do not provide the EXPECTED solution.
=================
Dear visitor,
I have read your comment regarding this problem, which you submitted to the @greenestamps' personal page.
Especially attentively, I read that part of your comment, which related to my solution.
It helped me to understand better your style of thinking and your style of making communication/discussion.
Be sure that I will make all my necessary conclusions from it for the future.
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The formula for the surface area of a sphere, and the units you use in your calculations, are irrelevant to the problem.
Surely the intent of the problem is to help you learn a very powerful general geometric principle:
If the scale factor (ratio of linear measurements) between similar figures is A:B, then the ratio of area measurements in the two figures is A^2:B^2, and the ratio of volume measurements in the two figures is A^3:B^3.
In this problem, your are given that the ratio of surface areas of two spheres is 2:1. In terms of the geomtric principle, that is the "A^2:B^2; and in the problem we are supposed to determine the ratio of linear measurements, which is the "A:B".
Since the ratio of surface areas in the two similar figures is 2:1, the ratio of the diameters (linear measurements) is  . .
ANSWER: the diameter must be altered by a factor of  . .
|
|
|