SOLUTION: Hello. I am unsure how to solve this: What is the smallest positive number for 3sin(2x-6)=1 the correct answer is: 0.028328455 (i looked it up on google). To solve this

Algebra ->  Trigonometry-basics -> SOLUTION: Hello. I am unsure how to solve this: What is the smallest positive number for 3sin(2x-6)=1 the correct answer is: 0.028328455 (i looked it up on google). To solve this       Log On


   

Question 1203148: Hello. I am unsure how to solve this:
What is the smallest positive number for
3sin(2x-6)=1
the correct answer is: 0.028328455 (i looked it up on google).
To solve this problem, i brought over the 3. so the equation would become sin(2x-6)=1/3. Then i brought the sin to the right side so the equation looked like this 2x-6=sin^-1(1/3). then i carried the 6 over so it became 2x=(sin^-1(1/3))+6 and then i divided the whole equation on the left side by 2 so i can solve for x. However, by doing so, it gave me an answer of about 12.7356
thank you
Answer by ikleyn(52900) About Me  (Show Source):
You can put this solution on YOUR website!
.

3*sin(2x-6) = 1  --->


sin(2x-6) = 1/3


2x-6 = arcsin(1/3) = 0.339837  or  2x-6 = pi - arcsin(1/3) = 3.14159 - 0.339837 = 2.801753.


2x = 0.339837 + 6 = 6.339837   or  2x = 2.801753 + 6 = 8.802.


From this value of 2x = 6.339837 we can (and, therefore, we should) subtract 2pi as many times, 
until we still get a positive number.

    6.339837 - 2*3.14159 = 0.056657.


It is the other, still valid candidate for 2x: geometrically, 
it represents THE SAME ANGLE (in radians) as 2x = 6.339837.


    +---------------------------------------------------------------------+
    |  In other words, we can say that the angle of 2x = 6.339837 radians |
    |       is equivalent to the angle of 0.056657 radians.               |
    +---------------------------------------------------------------------+


So, to get x, we divide the value of 0.056657 by 2

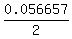    0.056657%2F2 = 0.0283285 radians,

which is close to the answer.

----------------

The lesson to learn from my post is this: 

    Geometrically, the numbers in radians, that are different 
    by the value of 2pi, represent the  SAME  ANGLE.

    So, for us such numbers, representing angles, are equivalent.
    This understanding is a key for solving this problem and many other similar problems.


////////////////////


Alternatively, you may look into my other (very similar) solution to this problem

https://www.algebra.com/algebra/homework/logarithm/logarithm.faq.question.1188985.html

which I provided at this forum several years ago.