SOLUTION: The area between y=x² and y+x²=8 is rotated 360° about the x-axis. Find the volume produced

Algebra ->  Test -> SOLUTION: The area between y=x² and y+x²=8 is rotated 360° about the x-axis. Find the volume produced      Log On


   

Question 1203141: The area between y=x² and y+x²=8 is rotated 360° about the x-axis. Find the volume produced
Answer by ikleyn(52887) About Me  (Show Source):
You can put this solution on YOUR website!
.
The area between y=x² and y+x²=8 is rotated 360° about the x-axis.
Find the volume produced
~~~~~~~~~~~~~~~~~~ 

The outer boundary is y = 8-x^2.

The inner boundary is y = x^2.


These two curves intersect when  

    8-x^2 = x^2,  8 = x^2+x^2,  8 = 2x^2,  x^2 = 8/2 = 4,  x = sqrt%284%29 = +/- 2.


In the interval  -2 <= x <= 2, both curve are above the x-axis.


Each vertical section  x= const  of this volume  (of this solid body)  is a RING 
with the inner radius  r= x^2  and the outer radius R = 8-x^2.


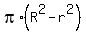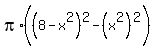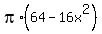The area of this ring is  pi%2A%28R%5E2-r%5E2%29 = pi%2A%28%288-x%5E2%29%5E2+-+%28x%5E2%29%5E2%29 = pi%2A%2864+-+16x%5E2%29.


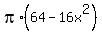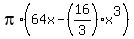The antiderivative is  of this function  pi%2A%2864-16x%5E2%29  is  F(x) = pi%2A%2864x+-+%2816%2F3%29%2Ax%5E3%29.  


The integral from  -2  to  2  is the difference  

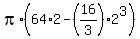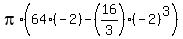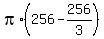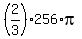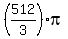    F(2) - F(-2) = (pi%2A%2864%2A2+-+%2816%2F3%29%2A2%5E3%29) - (pi%2A%2864%2A%28-2%29+-+%2816%2F3%29%2A%28-2%29%5E3%29) = pi%2A%2864%2A4+-+2%2A%2816%2F3%29%2A8%29 = pi%2A%28256-256%2F3%29 = %282%2F3%29%2A256%2Api = %28512%2F3%29pi.


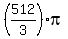Thus the desired volume is  %28512%2F3%29pi = %28512%2F3%29%2A3.14159265 = 536.1651  (rounded).    ANSWER

Solved.