|
Question 1203123: A quadrilateral has vertices at P (-8, 15), Q (10, 11), R (12, -1), and S (-4, -9)
a.) What shape is this quadrilateral?
b.) Do the diagonals bisect each other?
c.) What shape is formed by connecting the midsegments? (midsegment is a line that connects midpoints)
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! A quadrilateral has vertices at
P ( , ,  ), Q ( ), Q ( , ,  ), R ( ), R ( , , ), and S ( ), and S ( , ,  ) )
a.) What shape is this quadrilateral?

it could be a trapezoid or a trapezium
a trapezoid when it has equal angles from a parallel side
a trapezium is a quadrilateral with NO parallel sides
check if  and and 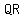 are a pair of are a pair of 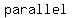 sides sides
Find the slope of the line through the points  and and 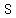 , and , and  and and 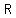 as well. as well.
if slopes are equal, than 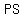 and and  are a pair of parallel sides are a pair of parallel sides
 slope is: slope is: 
and
 slope is: slope is: 
slopes are equal => 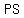 and and 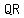 are a pair of parallel sides are a pair of parallel sides
so, we have a 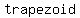
b.) Do the diagonals bisect each other?
a trapezoid can have only one pair of parallel sides, means that the diagonals do NOT bisect each other
c.) What shape is formed by connecting the midsegments? (midsegment is a line that connects midpoints)
first find midpoints of each side
P ( , ,  ), Q ( ), Q ( , ,  ), R ( ), R ( , , ), and S ( ), and S ( , ,  ) )
PQ: M1 ( , , 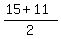 )=( )=( , ,  ) )
QR :M2 (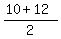 , , 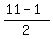 )=( )=( , ,  ) )
RS :M3 (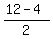 , , 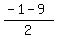 )=( )=( , ,  ) )
PS:M4 (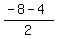 , , 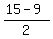 )=( )=( , ,  ) )

leaving for you to answer what shape is formed by connecting the midsegments
Answer by ikleyn(52900)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For any convex quadrilateral, its midpoints are vertices of a parallelogram.
For the proof (which is very simple), see the lesson
- Midpoints of a quadrilateral are vertices of the parallelogram
in this site.
It is a general property of any plane convex quadrilateral, independently on disposition/location of its vertices.
---------------
On Geometry, you have this free of charge online textbook
- GEOMETRY - YOUR ONLINE TEXTBOOK
in this site.
The referred lesson is the part of this textbook under the topic "PROPERTIES OF PARALLELOGRAMS".
Save the link to this online textbook together with its description
Free of charge online textbook in GEOMETRY
https://www.algebra.com/algebra/homework/Triangles/GEOMETRY-your-online-textbook.lesson
to your archive and use it when it is needed.
|
|
|
| |