Question 1202974: Hi,
Can you help me with the question below:
From a point P due south of a vertical tower, the angle of elevation of the top of the tower is 20 degrees . From a point Q situated 40 metres from P and due east of the tower, the angle of elevation is 35 degrees . Let h metres be the height of the tower.
a. Draw a diagram to represent the situation.
b. Evaluate h correct to the nearest metre
Thank you
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hi,
Can you help me with the question below:
From a point P due south of a vertical tower, the angle of elevation
of the top of the tower is 20 degrees .
From a point Q situated 40 metres from P and due east of the tower,
the angle of elevation is 35 degrees . Let h metres be the height of the tower.
a. Draw a diagram to represent the situation.
b. Evaluate h correct to the nearest metre
Thank you
~~~~~~~~~~~~~~~~~~~
I will not make a diagram for you, since I assume that it is your job.
I will solve the problem, instead.
The distance from the base of the tower to point P horizontally in the southern direction is
 = = 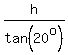 .
The distance from the base of the tower to point Q horizontally in the eastward direction is .
The distance from the base of the tower to point Q horizontally in the eastward direction is
 = = 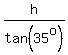 . .
 and and  are the legs of a right angled triangle, whose hypotenuse is 40 meters.
So, we write the Pythagorean equation are the legs of a right angled triangle, whose hypotenuse is 40 meters.
So, we write the Pythagorean equation
 + +  = =  . (1)
Substituting the values of tan(20°) = 0.363970 and tan(35°) = 0.70021 and making all necessary calculations,
I reduce equation (1) to
7.548642*h^2 + 2.03959*h^2 = 1600,
or 9.588234*h^2 = 1600,
which gives h = . (1)
Substituting the values of tan(20°) = 0.363970 and tan(35°) = 0.70021 and making all necessary calculations,
I reduce equation (1) to
7.548642*h^2 + 2.03959*h^2 = 1600,
or 9.588234*h^2 = 1600,
which gives h =  = 12.92 meters.
Rounding to the nearest meter, I get the ANSWER h = 13 meters. = 12.92 meters.
Rounding to the nearest meter, I get the ANSWER h = 13 meters.
Solved.
|
|
|