Question 1202955: A given sinusoidal function has a period of 3, an amplitude of 7, and a maximum at (0, 2). Represent the function with a sine equation and a cosine equation.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the general form of the sine and cosine function is y = a * sin(b * (x - c)) + d or y = a * cos(b * (x - c)) + d.
a is the amplitude.
b is the frequency.
c is the horizontal shift.
d is the vertical shift.
since the amplitude is 7, the general form becomes y = 7 * sin(b * (x - c)) + d or y = 7 * cos(b * (x - c)) + d.
when d = 0, the horizontal center line of the graph is at y = 0.
if the horizontal center line of the graph is at y = 0, then the max value of the graph will be at y = 7 and the min value of the graph will be at y = -7.
since the max value of the graph is at (0,2), then the max value of the graph is at y = 2.
subtract 7 from that to get a horizontal center line at y = -5.
this means that d must be equal to -5, since d gives you the vertical shift of the graph horizontal center line.
the general form of the graph now becomes y = 7 * sin(b * (x - c)) - 5 or y = 7 * cos(b * (x - c)) - 5.
the period of the graph is 3.
since the frequency of the graph is equal to 360 / period, then the frequency of the graph must be equal to 120.
this means that you will get 120 full cycles of the sine or cosine graph in the normal period of 360 degrees.
the general form of the graph now becomes y = 7 * sin(120 * (x - c)) - 5 or y = 7 * cos(120 * (x - c)) - 5.
you are given that the graph has a maximum at (0,2).
this means that the high peak of the graph is at 2 when the value of x is at 0.
since the cosine function normal cycle has a peak at x = 0, then there is no horixontal shift of the cosine function.
the general form of the graph now becomes y = 7 * sin(120 * (x - c)) - 5 or y = 7 * cos(120 * x) - 5.
the c disappears in the cosine graph because the shift is equal to 0.
the sine function peaks at x = 90 degrees when the period is 360 degrees.
to make the sine function pack at 0 degrees, the graph of the sine function must be shifted to the left 90 degrees.
that is when the peiod is 360 degrees.
when the period is 3 degrees, the shift is equal to 90 / 120 = .75 degrees.
the general form of the graph now becomes y = 7 * sin(120 * (x - .75)) - 5 or y = 7 * cos(120 * x) - 5.
these are the final forms of the graph and should satisfy the reqirements of the problem.
the graph is shown below.
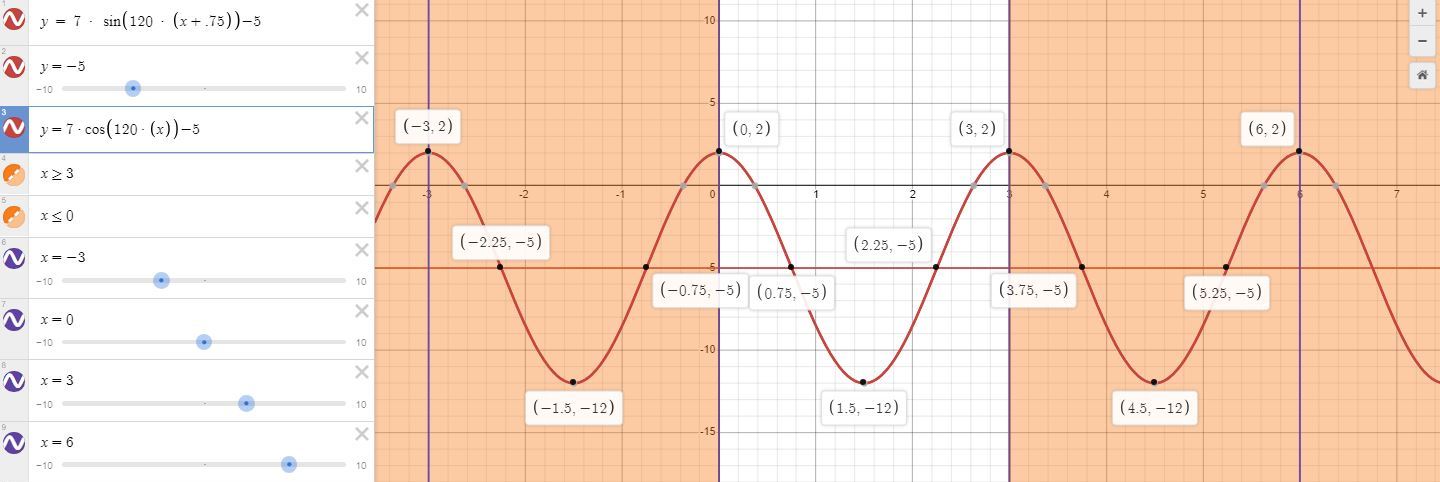
both sine and cosine graphs are shown.
since they are equivalent, they both draw the same image on the graph.
3 periods of both functions are shown.
the main, or base period is from x = 0 to x = 3
the period before is from x = -3 to x = 0
the period after is from x = 3 to x = 6
the horizontal center line is at y = -5
the high value of the graph is at y = 2
the low value of the grpah is at y = -12
|
|
|