Question 1202927: CalJuice Company has decided to introduce three fruit juices made from blending two or more concentrates. These juices will be packaged in 2-qt (64-oz) cartons. One carton of pineapple-orange juice requires 8 oz each of pineapple and orange juice concentrates. One carton of orange-banana juice requires 12 oz of orange juice concentrate and 4 oz of banana pulp concentrate. Finally, one carton of pineapple-orange-banana juice requires 4 oz of pineapple juice concentrate, 8 oz of orange juice concentrate, and 4 oz of banana pulp concentrate. The company has decided to allot 16,000 oz of pineapple juice concentrate, 24,000 oz of orange juice concentrate, and 5000 oz of banana pulp concentrate for the initial production run. The company also stipulated that the production of pineapple-orange-banana juice should not exceed 800 cartons. Its profit on one carton of pineapple-orange juice is $1.00, its profit on one carton of orange-banana juice is $0.80, and its profit on one carton of pineapple-orange-banana juice is $0.90. To realize a maximum profit, how many cartons of each blend should the company produce?
pineapple-orange juice ____ cartons
orange-banana juice ___ cartons
pineapple-orange-banana juice 800 cartons
What is the largest profit it can realize?
$ ______
Are there any concentrates left over? (If so, enter the amount remaining. If not, enter 0.)
pineapple concentrate
0 oz
orange concentrate
0 oz
banana pulp concentrate
____ oz
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i used the simplex method calculator at https://www.zweigmedia.com/RealWorld/simplex.html
my constraint and objective chart is shown below:
A B C
pineapple concentrate 8 0 4 <= 16000 ounces
orange juice concentrate 8 12 8 <= 24000 ounces
banana pulp concentrate 0 4 4 <= 5000 ounces
profit 1 0.8 0.9 maximize dollars
this is what the results from the simplex method calculator look like.
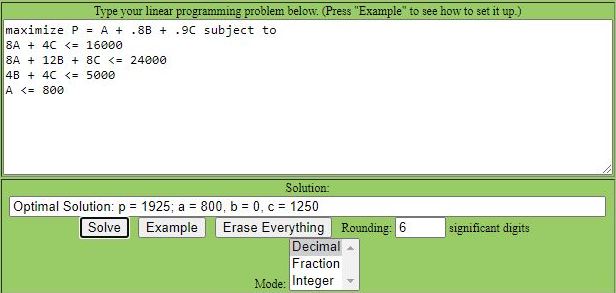
the solution states that the maximum profit is made when 800 cartons of type A and 1250 cartons of type C mixture are made and sold.
no cartons of type B mixture were made and sold, according to the calculator.
i duplicated the problem in excel and it gave me the same solution.
type A mixture is a pineapple orange juice concentrate blend
type B mixture is an orange juice banana pulp concentrate blend
type C misture is a pineapple orange juice banana pulp concentrate blend
each carton contains 48 ounces of water to mix with the concentrate for a total of 64 ounces per carton.
the profit is based on 1 dollar per type A carton plus 80 centers per type B carton plus 90 cents per type C carton.
the number of ounces of pineapple concentrate used was 800 * 8 + 1250 * 4 = 11400.
the amount left over was 16000 minus 11400 = 4600.
the number of ounces of orange juice concetnrate used was 800 * 8 + 1250 * 8 = 16400.
the amount left over was 24000 minus 16400 = 7600.
the number of ounces of banana pulp used was 1250 * 4 = 5000
the amount left over was 5000 minus 5000 = 0.
the maximum profit was 800 * 1 + 1250 * .9 = 1925 dollars.
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! . 1202927
CalJuice Company has decided to introduce three fruit juices made from blending two or more concentrates.
These juices will be packaged in 2-qt (64-oz) cartons.
One carton of pineapple-orange juice requires 8 oz each of pineapple and orange juice concentrates.
One carton of orange-banana juice requires 12 oz of orange juice concentrate and 4 oz of banana pulp concentrate.
Finally, one carton of pineapple-orange-banana juice requires 4 oz of pineapple juice concentrate,
8 oz of orange juice concentrate, and 4 oz of banana pulp concentrate.
The company has decided to allot 16,000 oz of pineapple juice concentrate, 24,000 oz of orange juice concentrate,
and 5000 oz of banana pulp concentrate for the initial production run.
The company also stipulated that the production of pineapple-orange-banana juice should not exceed 800 cartons.
Its profit on one carton of pineapple-orange juice is $1.00, its profit on one carton of orange-banana juice is $0.80,
and its profit on one carton of pineapple-orange-banana juice is $0.90.
To realize a maximum profit, how many cartons of each blend should the company produce?
pineapple-orange juice ____ cartons
orange-banana juice ___ cartons
pineapple-orange-banana juice 800 cartons
What is the largest profit it can realize?
$ ______
Are there any concentrates left over? (If so, enter the amount remaining. If not, enter 0.)
pineapple concentrate
0 oz
orange concentrate
0 oz
banana pulp concentrate
____ oz
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution to this problem in the post by @Theo is incorrect.
Indeed, his solution states
the maximum profit is made when 800 cartons of type A and 1250 cartons of type C mixture are made and sold.
no cartons of type B mixture were made and sold.
Then the maximum profit is 800*1 + 1250*0.9 = 1925 dollars.
I will disprove @Theo' solution right now.
For it, I will present another possible solution, which provides greater profit
and still does satisfy the restrictions.
This solution is 2000 cartoons of pineapple-orange juice and 0 cartons for two other juice.
It requires 2000*8 = 16000 oz of pineapple concentrate (which is under restriction)
and 2000*8 = 16000 oz of orange concentrate (which is also under restriction).
But the profit in this case is 1*2000 = 2000 dollars, which is GREATER than 1925 dollars in the @Theo' solution.
Thus I disproved the @Theo solution - - - it does not provide the optimum strategy.
Now, as I proved that the solution in the post by @Theo is incorrect,
I will present my analysis below.
Let x be the number of cartons of pineapple-orange PO-juice;
y be the number of cartons of orange-banana OB-juice;
z be the number of cartons of pineapple-orange-banana POB-juice.
One carton PO-juice = (8 oz P, 8 oz O ).
One carton OB-juice = ( 12 oz O, 4 oz B).
One carton POB-juice = (4 oz P, 8 oz O, 4 oz B).
We want to maximize the profit function P = x + 0.8y + 0.9z dollars.
The restrictions are
8x + 4z <= 16000 (pineapple juice concentrate restriction, in oz);
8x + 12y + 8z <= 24000 (orange juice concentrate restriction, in oz);
4y + 4z <= 5000 (banana pulp concentrate, in oz).
z <= 800,
x >= 0, y >= 0, z >= 0.
I will solve the problem using the simplex method and the online solver at this web-site
https://www.zweigmedia.com/RealWorld/simplex.html
(the same solver, as @Theo used).
It requires the input information be presented in its special format, which you may find
in the description to the solver.
So, the formatted input information for the solver is this
maximize p = x + 0.8y + 0.9z subject to
8x + 4x <= 16000
8x + 12y + 8z <= 24000
4y + 4z <= 5000
z <= 800,
x >= 0,
y >= 0,
z >= 0.
I copy-paste it into the solver.
After one click, the solver generates this OPTIMAL SOLUTION
p = 2640; x = 1600, y = 400, z = 800.
Having it, you can answer all remaining questions.
|
|
|