Question 1202906: A student takes ten questions which are true or false. one mark is even for each question. Find the probability that the student will obtain passing grade 60% or greater simply by guessing
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The probability of getting n out of 10 correct by guessing is 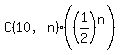 . .
So the answer to the problem is

To find this sum, you can...
(a) use a calculator;
(b) calculate all those C(10,n) values and add them; or
(c) write out the 10th row of Pascal's Triangle
Assuming you are not using a calculator, option (c) is far faster then option (b)... IF you know how to write out a row of Pascal's Triangle.
If you haven't seen that before, here is how to write out the 10th row of Pascal's Triangle. (Use the same process to write out any number of entries in any row of Pascal's Triangle.)
The first two entries in row n of Pascal's Triangle are 1 and n. The first two entries in row 10 are 1 and 10. For purposes of this demonstration, the 10 is obtained by multiplying the 1 by (10/1).
Then to write out the complete row 10 of Pascal's Triangle....
1st entry: 1
2nd entry: 1st entry, multiplied by (10/1) --> 1(10) = 10
3rd entry: 2nd entry, multiplied by (9/2) --> 10*(9/2) = 45
4th entry: 3rd entry, multiplied by (8/3) --> 45*(8/3) = 120
5th entry: 4th entry, multiplied by (7/4) --> 120(7/4) = 210
6th entry: 5th entry, multiplied by (6/5) --> 210(6/5) = 252
7th entry: 6th entry, multiplied by (5/6) --> 252(5/6) = 210
The pattern of multipliers should be clear. You can also see why the pattern is what it is by comparing, for example, the formal calculations of C(10,3) and C(10,4):


The difference between the two calculations is the additional factor (7/4); so C(10,4) = C(10,3) multiplied by (7/4).
Since you know the entries in each row are symmetrical, the 10th row of Pascal's Triangle is
1 10 45 120 210 252 210 120 45 10 1
Now to use that to solve the given problem.
The entries corresponding to getting 10, 9, 8, 7, or 6 correct are
1 10 45 120 210
The answer to the problem is then
ANSWER: 
Simplify or convert to decimal form if needed.
|
|
|