Question 1202897: . (a) A bag contains 16 identical balls of which 4 are green. A boy picks a ball at random from the bag and replaces it. If this is repeated 5 times, what is the probability that he: (i) did not pick a green ball: (ii) picked a green ball at least three times?
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(i) The probability of getting green on each draw is 4/16 = 1/4, so the probability of not getting green is 3/4. The probability of not getting green 5 times in a row is
(3/4)^5 = 243/1024
(ii) The probability of getting green on each draw is 1/4; the probability of getting another color is 3/4. If "Y" (yes) represents drawing a green ball and "N" (no) represents getting a color other than green, then the "probability vector" for each draw is
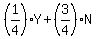
If the draw is repeated 5 times, the probability vector is
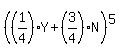
For this question, we want the probability of getting a green ball at least 3 times -- i.e., either 3, 4, or 5 times.
This is binomial probability; the computations are straightforward but tedious, so I'm not going to do them for you.
To get the answer, you need to perform these three calculations and add the results:
3 green: 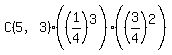
4 green: 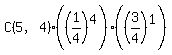
5 green: 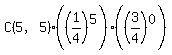
Note the answer to (i) can be found using this same kind of binomial probability calculation:
0 green: 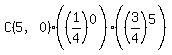
But that calculation simplifies to just (3/4)^5, which is the answer shown above.
|
|
|