Question 1202803: Sally Sethness assembles stereo equipment for resale in her shop. She offers two products, turntables and cassette players. She makes a profit of $10 on each turntable and $6 on each cassette. Both must go through two steps in her shop—assembly and bench checking. A turntable takes 12 hours to assemble and 4 hours to bench check. A cassette player takes 4 hours to assemble but 8 hours to bench check. Looking at this month's schedule, Sally sees that she has 60 assembly hours uncommitted and 40 hours of bench-checking time available. Use graphic linear programming to find her best combination of turntables and cassette players. What is the total profit on the combination you found?
Found 3 solutions by Theo, ikleyn, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = number of turntables
y = number of cassette players
objecive function if profit.
profit = 10x + 6y
assembly constraints are:
12x + 4y <= 60
bench test constraints are:
4x + 8y <= 40
x >= 0
y >= 0
using the desmos.com calculator, you would graph the opposite of the constraints.
the area not shaded is the region of feasibility.
you would then evaluate the profit at the corner points of this feasible region to find the corner point with the maximum profit.
corner points are (0,5), (4,3), (5,0).
maximum profit is 58 at (4,3)
all constraints are satisfied at that point, as they need to be.
desmos.com calculator is at https://www.desmos.com/calculator
here's what the graph looks like.

Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Sally Sethness assembles stereo equipment for resale in her shop.
She offers two products, turntables and cassette players.
She makes a profit of $10 on each turntable and $6 on each cassette.
Both must go through two steps in her shop—assembly and bench checking.
A turntable takes 12 hours to assemble and 4 hours to bench check.
A cassette player takes 4 hours to assemble but 8 hours to bench check.
Looking at this month's schedule, Sally sees that she has 60 assembly hours uncommitted
and 40 hours of bench-checking time available.
Use graphic linear programming to find her best combination of turntables and cassette players.
What is the total profit on the combination you found?
~~~~~~~~~~~~~~~~~~~~~
Let X be the number of turntable and Y be the number of cassette players.
We want maximize the profit function
P(X,Y) = 10X + 6Y
under the following restrictions
12X + 4Y <= 60 (assembly time)
4X + 8Y <= 40 (bench check time)
X >= 0, Y >= 0
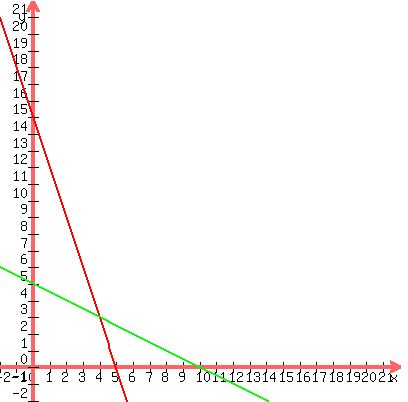
The plot of the feasibility domain is shown in the Figure below.
 Plots y =
Plots y = 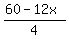 (red) and y = (red) and y = 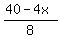 (green)
It is a quadrilateral in QI with the vertices at points P1 = (0,0), P2 = (0,5), P3 = (4,3), P4 = (5,0).
We apply the standard Linear Programming method in its geometric interpretation.
The solution is one of these 4 points, where the objective function (profit) has a maximum.
You calculate the values of the objective function P(X,Y) (profit) at listed points
P1: P(0,0) = 10*0 + 6*0 = 0,
P2: P(0,4) = 10*0 + 6*5 = 30,
P3: P(4,3) = 10*4 + 6*3 = 58,
P4: P(6,0) = 10*5 + 6*0 = 50.
Comparing these values, you find the optimal point.
It is P3: (X,Y) = (4,3), which means 4 turntables and 3 cassette players, providing maximum PROFIT of 58 dollars. (green)
It is a quadrilateral in QI with the vertices at points P1 = (0,0), P2 = (0,5), P3 = (4,3), P4 = (5,0).
We apply the standard Linear Programming method in its geometric interpretation.
The solution is one of these 4 points, where the objective function (profit) has a maximum.
You calculate the values of the objective function P(X,Y) (profit) at listed points
P1: P(0,0) = 10*0 + 6*0 = 0,
P2: P(0,4) = 10*0 + 6*5 = 30,
P3: P(4,3) = 10*4 + 6*3 = 58,
P4: P(6,0) = 10*5 + 6*0 = 50.
Comparing these values, you find the optimal point.
It is P3: (X,Y) = (4,3), which means 4 turntables and 3 cassette players, providing maximum PROFIT of 58 dollars.
Solved.
--------------
If you want to see many other similar and different solved problems, look into the lesson
- Solving minimax problems by the Linear Programming method
in this site.
/////////////////////
In opposite to Calculus, which was invented about three hundred years ago,
the Linear Programming method for solving linear min-max problems
was invented about only 80 years ago, in 1940'.
It quickly became widely accepted and widely extended method
of solving many important problems in Economics.
The size of solved problems quickly increased from tens to hundreds,
thousands and more variables. The best mathematical minds took part
in creating and developing this method.
So, now this method is studied in high schools, colleges, and universities.
There are several levels of learning/teaching this method.
First, the lowest/starting level is its geometric version, as I presented it
in my post. At this level, students learn it in high school.
Usually, only two unknown variables are considered, and the purpose of
this learning is to make first steps: to get a first acquaintance
with the method, to get its idea, and to get familiarity on how it works.
The major idea of the LP-method is that linear function over a polyhedron
in multi-dimensional linear space gets its maximum-minimum values
at the corners/vertices of the polyhedron.
The idea is simple, but enormously productive.
The second level is advanced consideration of the 2D case with two unknowns
and 3D case. At this level, it is appropriate to consider version of the method
with slopes of the constraint boundary lines and the slope of the objective function.
It is the level of teaching this method in colleges, where Math is not a major specialty.
Third level is teaching students to use existing standard calculators
from the Internet, like Theo does it in his post.
This third level can sometimes be combined with the first or the second level.
At this level, the major goal is to teach students to setup problems.
Fourth level is studying this method in the matrix version, oriented
for work with thousands unknowns. It is intended for those students who are
going/targeted to be the upper level users and/or professional DEVELOPERS
in this area. It is the level of renowned Math colleges and Universities,
and the level of graduate students, working on their PhD degrees in the area.
In the pedagogic literature, these levels are strictly separated.
There are, probably, tens of textbooks for the first level;
there are textbooks for the second level, although not so many.
On my bookshelf, I have three college Math textbooks teaching at this level,
and I am sure that every student, who really needs and wants to know
the subject at this level, has an ability to learn from such textbooks.
Always there is a possibility to buy affordable used textbook for low price,
since at this level nothing is changed in decades.
(And, empirically, than older is a textbook, than it is better).
For the highest, fourth level, there are standard textbooks and monographs
on simplex method, as well as Proceedings of numerous conferences.
They are used by PhD students in their Computer Science courses or in
their Computational Math courses. And at the level 4, the simplex method technically
has nothing in common with the levels 1, 2 and 3, except of general idea.
So, regarding the LP-method or simplex method, there are enough educational sources
for each level, and they are strictly/accurately separated by levels of complexity.
Next, when students come to this forum asking to enlighten them about the LP-method,
such requests are 100% from beginner students, who need to get basic knowledge at level number one.
As soon as they know the subject at this level one, they will not come to this forum
asking to enlighten them at level two: they will go further on their own legs,
without spikes/toggles.
It is why I always present them the LP-method at the level one, as I did it in my post above.
Not because I am a bad or a limited person, but because the life is arranged this way, and not otherwise.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn has provided a complete detailed description of the standard solution method, so look at her response for a good solution.
However, there is a shortcut to the solution which can be a big time saver if the linear programming problem is more complex -- for example, a problem having three or even more constraints instead of the standard two.
Virtually all resources on linear programming, including the link on this site she references in her response, say that to find the maximum or minimum value of the objective function you need to evaluate the function at all corners of the feasibility region.
That is not true.
The corner of the feasibility region where the objective function is maximum or minimum can be determined by comparing the slope of the objective function to the slopes of the constraint boundary lines. Geometrically, what you are doing with this process is finding where a line with the slope of the objective function just touches the feasibility region.
In this problem, the slopes of the constraint boundary lines are -1/2 and -3; the slope of the objective function is -5/3. Since -5/3 is between -1/2 and -3, the objective function value will be maximized at the intersection of the two constraint boundary lines.
Part of the standard process, a shown in her response, is to find the corners of the feasibility region, which involves solving pairs of equations of the constraint boundary lines. In this problem, with two constraints, there is just one such intersection, so doing the algebra to find that single intersection is not much work. But in a more complex problem with more constraints, it would be a lot of work to find all the intersection points.
Using this method of comparing the slopes of the lines means you always know where the objective function will be maximized, so you only have to find one of the points of intersection of the constraint boundary lines.
In this problem, the intersection of the two constraint boundary lines is at (4,3), so the objective function is maximized when she produces 4 turntables and 3 cassette players; the maximum profit is 4($10)+3($6) = $40+$18 = $58.
|
|
|