Question 1202779: A tube of Listerine Tartar Control toothpaste contains 4.2 ounces. As people use the toothpaste, the amount remaining in any tube is random. Assume the amount of toothpaste remaining in the tube follows a uniform distribution. From this information, we can determine the following information about the amount remaining in a toothpaste tube without invading anyone’s privacy.
a. How much toothpaste would you expect to be remaining in the tube?
b. What is the standard deviation of the amount remaining in the tube?
c. What is the likelihood there is less than 3.0 ounces remaining in the tube?
d. What is the probability there is more than 1.5 ounces remaining in the tube?
Answer by ikleyn(52812)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A tube of Listerine Tartar Control toothpaste contains 4.2 ounces.
As people use the toothpaste, the amount remaining in any tube is random.
Assume the amount of toothpaste remaining in the tube follows a uniform distribution.
From this information, we can determine the following information about
the amount remaining in a toothpaste tube without invading anyone’s privacy.
a. How much toothpaste would you expect to be remaining in the tube?
b. What is the standard deviation of the amount remaining in the tube?
c. What is the likelihood there is less than 3.0 ounces remaining in the tube?
d. What is the probability there is more than 1.5 ounces remaining in the tube?
~~~~~~~~~~~~~~~~~~~~~~
Many mathematical problems are specially presented by their authors as a verbal compote,
and if you don't understand how to approach to such tasks, it means that you have been drowned
in this verbal compote. So, your first task is to filter out the water until you get a dry residue.
It is your first and most important step in solving such problems.
If you apply this method to the given problem, then the dry residue is THIS:
Let X be the amount of the toofpaste remaining in the tube.
X is a random variable uniformly distributed on the interval [0,4.2].
(a) Find the Math Expectation of X.
(b) Find the standard deviation of X.
(c) Find the probability P(X < 3).
(d) Find the probability P(X > 1.5).
The answers are simple: they are based on standard properties of a uniform distribution,
that are written in any relevant textbook. It is your assumed pre-requisite to know these properties.
(a) Math Expectation of X is 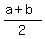 = = 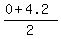 = = 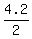 = 2.1.
In meaningful context, you may expect about 2.1 ounses of the
remaining Listerine Tartar Control toothpaste in the tube.
(b) The standard deviation is = 2.1.
In meaningful context, you may expect about 2.1 ounses of the
remaining Listerine Tartar Control toothpaste in the tube.
(b) The standard deviation is 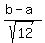 = = 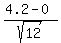 = = 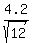 = 1.2124 ounces (rounded).
(c) P(X < 3) = = 1.2124 ounces (rounded).
(c) P(X < 3) = 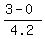 = = 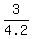 = 0.7143 (rounded).
(d) P(X > 1.5) = = 0.7143 (rounded).
(d) P(X > 1.5) = 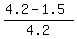 = = 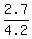 = 0.6429 (rounded). = 0.6429 (rounded).
At this point, the problem is solved and the solution is complete.
-----------------
The post-solution note
The lesson to learn from my post is the method of filtering out
water from a verbal compote till getting a dry residue.
|
|
|