Question 1202738: A classmate offers a game for you to play. You roll a single six-sided die, and if the roll is 3 or higher, you win $3. If you roll a 1 or a 2, you owe him $2. Little do you know, the die is loaded. The probability that you'll roll a 1 is 0.53, and the rest of the values have equal probabilities. What is the expected value of this game?
Answer by ikleyn(52795)   (Show Source):
You can put this solution on YOUR website! .
A classmate offers a game for you to play. You roll a single six-sided die,
and if the roll is 3 or higher, you win $3. If you roll a 1 or a 2, you owe him $2.
Little do you know, the die is loaded. The probability that you'll roll a 1 is 0.53,
and the rest of the values have equal probabilities. What is the expected value of this game?
~~~~~~~~~~~~~~~~~~~~
From the condition, the probability density distribution function is
P(1) = 0.53; P(2) = P(3) = P(4) = P(5) = P(6) = 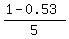 = 0.094.
Therefore, the expected value of the game is
-2*P(1) - 2*P(2) + 3*(P(3)+P(4)+P(5)+P(6)) = -2*0.53 - 2*0.094 + 3*4*0.094 = -0.12 dollars.
It means that you will lose 12 cents, in average, in each game, if you play this game many times.
Solved, with complete explanations.
|
|
|
