Question 1202648: Bob and his brother Jim live 95 miles apart and like to meet and play golf together, the course is 15 miles further for Bob as it is from Jim but Bob averages 10 mph faster than Jim so if they want to meet at the course at 9:00 and Jim leaves at 8:00 what time would Bob need to leave?
Found 3 solutions by mananth, ikleyn, math_tutor2020:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Bob and his brother Jim live 95 miles apart and like to meet and play golf together, the course is 15 miles further for Bob as it is from Jim but Bob averages 10 mph faster than Jim so if they want to meet at the course at 9:00 and Jim leaves at 8:00 what time would Bob need to leave?
Jim's distance = 15 miles
Time taken by Jim = 1 hour (8.00 to 9.00)
Jim's speed = 15 mph
Bob's speed = 15+10 =25 mph
Bob has to travel 95+15 = 110 miles
t =d/s
110/25 = 4.4 hour
Bob has to leave 3.4 hours earlier than Jim
0.4 hour = 24 minutes
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Bob and his brother Jim live 95 miles apart and like to meet and play golf together,
the course is 15 miles further for Bob as it is from Jim but Bob averages 10 mph faster
than Jim so if they want to meet at the course at 9:00 and Jim leaves at 8:00
what time would Bob need to leave?
~~~~~~~~~~~~~~~~~~~~~
Let me make some/several notes as I read your post.
First, the assignment is written unprofessionally.
From the post, it is difficult to understand the meaning of the assignment:
it needs to be re-formulated to make it clear.
So, it is not suprised, that the other tutor @mananth reads, understands and
interprets it incorrectly; so, his solution is incorrect, too.
Second, in English, problem's writers and all other writers NEVER use so long
statements as in your post. They usually use punctuation signs like dots and
commas to subdivide their long thoughts into short understandable sentenses.
Also, professional writers tend to place their sentences in logic order,
because their goal is not to fool readers; in opposite, their goal is to teach
the students to present their own thoughts in logic form.
It is a necessary condition in order for the students love Math;
otherwise, they will hate it.
Therefore, below I place my formulation in the form as it should be.
Bob and Jim live 95 miles apart along a highway and like to meet and play golf together.
The golf course is located somewhere near the highway between the Bob's and Jim's homes
15 miles further from Bob's home as it is from Jim's home.
They want to meet at the course at 9:00 am. Jim leaves at 8:00 am.
Bob averages 10 mph faster than Jim. At what time would Bob need to leave?
Solution
First, from the condition it is clear that the distance from Bob's home to the golf course
is 55 miles, while that from the Jim's home to the golf course is 40 miles.
If it is not obvious for you, then you can write these equations for distances
B + J = 95 miles (1)
B - J = 15 miles (2)
and add them. You will get
2B = 95 + 15 = 110 miles ---> B = 110/2 = 55; then from equation (1) J = 95-55 = 40 miles.
+--------------------------------------------------------+
| OK. Half of the problem is just solved. |
| Starting from this point, I will work on other half. |
+--------------------------------------------------------+
Jim leaves at 8:00 am and arrives at 9:00 am - so, Jim spends precisely 1 hour for his trip.
It tells us that the Jim's average speed is 40 mph.
From it, we conclude that Bob's average speed is 40+10 = 50 mph.
So, Bob's travel time is 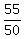 = 1 = 1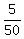 hours = 1 hours = 1 hours = 1 hour and 6 minutes.
It means that Bob should leave 6 minutes before 8:00 am, i.e. at 7:54 am.
ANSWER. Bob should leave at 7:54 am, or 6 minutes before Jim. hours = 1 hour and 6 minutes.
It means that Bob should leave 6 minutes before 8:00 am, i.e. at 7:54 am.
ANSWER. Bob should leave at 7:54 am, or 6 minutes before Jim.
Solved, with explanations.
------------------
As I see, tutor @math_tutor2020 successfully retold my solution in his own words.
I don't know, for what reason he did it. The solution did not become better of it.
In any case, thanks for popularizing my ideas.
As I worked in Science and Engineering for many years, I know that it is not welcome
(is not a good style) to re-told the published works of other people without a reference.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Draw a number line to mark these three locations- B = Bob's starting location
- G = golf course location
- J = Jim's starting location
We have these segment pieces:- GJ = x = distance from Jim to golf course
- BG = x+15 = distance from Bob to golf course
Those two pieces must add to the 95 mile gap between the two brothers. I'm assuming the golf course is between them.
GJ + BG = 95
x + (x+15) = 95
2x + 15 = 95
2x = 95-15
2x = 80
x = 80/2
x = 40
Jim travels x = 40 miles.
Bob travels x+15 = 40+15 = 55 miles.
Jim travels 40 miles in 1 hour, which is the time gap from 8:00 to 9:00.
Jim drives at 40 mph (average).
Formula is: rate = distance/time
40+10 = 50 mph is Bob's average speed.
Let's determine how long Bob would take to travel 55 miles at 50 mph.
distance = rate*time
time = distance/rate
time = 55/50
time = 1.10 hours
The 0.10 hour portion converts to 0.10*60 = 6 minutes
1.10 hours = 1 hour + 6 minutes
Bob is on the road for 6 additional minutes compared to his brother.
He'll need to rewind the clock 6 minutes into the past to be able to arrive at 9:00
8:00 - 6 minutes = 7:54
In other words,
7:54 + (1 hr & 6 min) = 9:00
Answer is 7:54
I'm not sure whether to put AM or PM. The instructions are vague about that. It could be possible that your teacher is using 24 hour time format.
|
|
|