Question 1202567: The sum of 2000 numbers is 2007. Find maximum product of these numbers. (There are more than one set of such numbers)
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
By a general principle, given a set of numbers with a particular sum, the maximum product of the numbers is when the numbers are all equal.
2000 numbers, all equal, with a sum of 2007, means each number is 2007/2000.
The maximum product is
ANSWER: 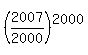 . .
Note the problem is not defined precisely enough. If some of the numbers are allowed to be negative, then there is no maximum product. Given a positive number x, the set consisting of -x, -1, 1997 1's, and x+11 has a sum of 2007, and the product of the numbers is x(x+11), which clearly has no maximum.
Answer by ikleyn(52816)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problem is worded, printed and presented INCORRECTLY in your post.
To be correct, it must say that all the considered numbers are positive.
Next incorrect statement is that "there are more than one set of such numbers ".
In OPPOSITE, there is ONLY ONE and UNIQUE such set of numbers.
When a Math problem comes with such flagrant errors,
a normal (and a natural) reaction of a reader is do not believe/(do not trust)
to any of its word and to any of its number.
|
|
|