Question 1202487: Word Problems involving Optimization (Derivatives)
A poster must have a printed area of 781.25 cm^2. It will have top and bottom margins that are 5 cm each and side margins that are 4 cm each. If all the dimensions of the printed area are at least 25 cm but at most 35 cm, what are the dimensions of the whole poster with the smallest total area? Show your solution.
Found 3 solutions by mananth, ikleyn, greenestamps:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!  . .
Area of poster A = (x+8)(y+10)
area printed xy
Printed area =781.25
y = 781.25/x
A= (x+8)((781.25/x)+10)
A =781.25 +10x +6250/x +80
The critical point occurs when dA(total)/dx =0
dA/dx = 10 -6250/x^2
10=6250/x^2
10x^2= 6250
x^2= 625
x = 25
y=35
Answer by ikleyn(52884)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by @mananth, giving the answer x= 25 cm, y= 35 cm,
is TOTALLY, ABSOLUTELY and FATALLY wrong,
since the product 25*35 = 875 cm^2 is not the required 781.25 cm^2 (the printed area).
Let x be horizontal and y be vertical dimension of the poster.
Then the printed area has dimensions (x-8) cm vertically and (y-10) cm horizontally.
We have these restrictions
25 cm <= x-8, y-10 <= 35 cm (1)
and
(x-8)*(y-10) = 781.25 cm^2. (2)
We want to minimize the product x*y, which is the area of the poster, under restrictions (1) and (2).
From restriction (2), we have
y - 10 = 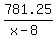 ,
or
y = ,
or
y = 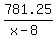 + 10. (3)
Then
xy = + 10. (3)
Then
xy =  + 10x.
Thus we want to find the minimum of this function
Z(x) = + 10x.
Thus we want to find the minimum of this function
Z(x) =  + 10x under restrictions 25 <= x-8, y-10 <= 35, where y = + 10x under restrictions 25 <= x-8, y-10 <= 35, where y = 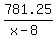 + 10.
Doing in accordance with the standard Calculus procedure, we should take the derivative
of function Z(x) and equate it to zero.
It leads us to equation + 10.
Doing in accordance with the standard Calculus procedure, we should take the derivative
of function Z(x) and equate it to zero.
It leads us to equation
 + 10 = 0,
from which we get + 10 = 0,
from which we get
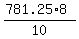 = = 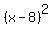 , , 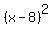 = 625, x-8 = = 625, x-8 = 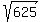 = 25, x = 33 cm,
and (x-8) satisfies the restriction 25 <= x-8 <= 35 cm.
Thus we solved the problem and found that the minimum area of the poster is achieved at x= 25 cm.
Then y = = 25, x = 33 cm,
and (x-8) satisfies the restriction 25 <= x-8 <= 35 cm.
Thus we solved the problem and found that the minimum area of the poster is achieved at x= 25 cm.
Then y = 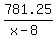 + 10 by formula (3), or y = + 10 by formula (3), or y = 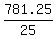 + 10 = 41.25.
We see that y satisfies the restriction 25 <= y-10 <= 35 cm.
Thus the answer is: optimum dimensions of the poster are x= 33 cm, y = 41.25 cm;
the minimal area of the poster is x*y = 33*41.25 = 1361.25 cm^2. + 10 = 41.25.
We see that y satisfies the restriction 25 <= y-10 <= 35 cm.
Thus the answer is: optimum dimensions of the poster are x= 33 cm, y = 41.25 cm;
the minimal area of the poster is x*y = 33*41.25 = 1361.25 cm^2.
Solved.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
While the answer from tutor @mananth is not correct, there is no need to disparage it, as the other tutor did. The solution is fine as far as it goes, except for the last careless calculation. And it doesn't complete the problem....
Without repeating the work that tutor @mananth shows....
x = 25
y = 781.25/25 = 31.25
The dimensions of the printed area are 25 by 31.25 cm.
The area of the whole poster, with margins 4 cm on the sides and 5 cm on top and bottom, is then either 35 by 39.25 cm or 33 by 41.25 cm.
By a general principle the second option gives the smaller area.
ANSWER: 33 by 41.25 cm
|
|
|