Question 1202441: Mrs. Green likes to serve two different kinds of vegetables with dinner. She has carrots, peas, okra, and green beans in her refrigerator . How many different sets of two vegetables can be serve? Tell wether this situation is a combination or permutation.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52913)   (Show Source):
You can put this solution on YOUR website! .
Mrs. Green likes to serve two different kinds of vegetables with dinner. She has carrots, peas, okra, and green beans
in her refrigerator . How many different sets of two vegetables can be serve? Tell wether this situation is a combination or permutation.
~~~~~~~~~~~~~~~~~~~~~~~
As the problem is written, it is CLEAR that the reader is just FAMILIAR
with conceptions of combinations and permutations and only wants to choose
correctly between these conceptions to solve the problem in a right way.
In this problem, the order of vegetables does not matter (at least, the problem
is silent about it, so by default and based on common sense, we can assume it).
If so, we use the conception of COMBINATIONS and do not use the conception of permutations.
The possible number of different combinations of 4 types of vegetables
taken two at a time is
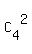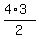 =  = 2*3 = 6.
The magic number of 4 is the number of different vegetables in her refrigerator.
Solved.
-------------------
On Combinations and Permutations, see introductory lessons
- Introduction to Permutations
- PROOF of the formula on the number of Permutations
- Simple and simplest problems on permutations
- Special type permutations problems
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
in this site.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
c = carrots
p = peas
o = okra
g = green beans
Let's make a table with 4 rows and 4 columns. Along the top and left side will be the letters mentioned
Assuming Mrs Green cannot select the same veggie twice, we cross off the items along the northwest (or southeast) diagonal.
For example, the upper left corner has "carrots" chosen twice.
Let's also cross off items below the diagonal. This is because the table has symmetry along the diagonal. An item below the diagonal will have a mirrored copy above the diagonal
There are 6 cells that haven't been crossed off, which is the final answer.
For instance, the left-most cell of the top row represents the combo "carrots and peas" in either order.
We started with a 4*4 = 16 cell table
Then subtracted off the four diagonal elements: 16-4 = 12
Cut that result in half (because we crossed out the lower half below the diagonal) to get 12/2 = 6
This division by two operation is to avoid double-counting.
The general formula is n*(n-1)/2 where n is a positive integer.
In this case we have n = 4 veggies to get n*(n-1)/2 = 4*(4-1)/2 = 6 combinations. Order doesn't matter.
A combo like "carrots and peas" is the same as "peas and carrots".
Notes: - An alternative pathway is to use the nCr combination formula with n = 4 and r = 2.
- Another path is to use Pascal's Triangle. Look at the row that starts with "1,4,..." and count over 3 spots to the right because the index starts at r = 0.
|
|
|
