.
a point moves on the parabola y^2=16x in such a way that the rate of change of the abscissa
is always 3 units/sec. how fast is the ordinate changing when the abscissa is 1 unit?
~~~~~~~~~~~~~~~~~~~~
The point (x,y) moves x = x(t), y = y(t) along the parabola
y^2 = 16x (1)
in such a way that the rate of change of the abscissa always is 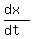 = 3 units/sec.
They want you find
= 3 units/sec.
They want you find  at x = 1.
It is easy. Take the derivatives respective the time "t" of the equation (1). You will get
at x = 1.
It is easy. Take the derivatives respective the time "t" of the equation (1). You will get
 =
=  , (2)
At x= 1, y^2 = 16, from equation (1). So, substitute in (2) y = +/-
, (2)
At x= 1, y^2 = 16, from equation (1). So, substitute in (2) y = +/- 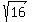 = +/- 4,
= +/- 4,  = 3, as it is given. You will get
2*(+/-4)*
= 3, as it is given. You will get
2*(+/-4)* =
= 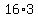 ,
which gives you
,
which gives you
 = +/- 6.
ANSWER. Under given conditions,
= +/- 6.
ANSWER. Under given conditions,  = +/- 6.
It means that when the point (x,y) moves on the upper branch y =
= +/- 6.
It means that when the point (x,y) moves on the upper branch y = 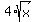 ,
,  = 6 at x= 1.
When the point (x,y) moves on the lower branch y =
= 6 at x= 1.
When the point (x,y) moves on the lower branch y = 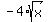 ,
,  = -6 at x= 1.
= -6 at x= 1.
Solved.