|
Question 1202332: A bus left an interchange carrying some passengers with it. At the first stop, 1/4 of the people in it alighted and 5 people boarded it. At the 2nd stop, 1/2 of the people in it alighted and 20 people boarded the bus. When it left the 2nd stop, there were 60 passengers in it. How many passengers were there in the bus when it left the interchange?
Found 3 solutions by mananth, MathTherapy, greenestamps:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! A bus left an interchange carrying some passengers with it. At the first stop, 1/4 of the people in it alighted and 5 people boarded it. At the 2nd stop, 1/2 of the people in it alighted and 20 people boarded the bus. When it left the 2nd stop, there were 60 passengers in it. How many passengers were there in the bus when it left the interchange?
Let there be x passengers at the interchange
At the first stop, 1/4 of the people in it alighted and 5 people boarded it.
x-(1/4)x +5
=x-(x/4)+5
= 3x/4 +5 were present when the bus left the First stop
At the 2nd stop, 1/2 of the people in it alighted and 20 people boarded the bus.
(3x/4 +5) - [1/2(3x/4+5) ) +20 =60
(3x/4 )- 3x/8 -5/2=35
3x/8 = 35+5/2
3x = 35*8+20
3x= 300
x= 100
100-25 +5 at the first stop= 80 remaining
80 -40 +20=60
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
A bus left an interchange carrying some passengers with it. At the first stop, 1/4 of the people in it alighted and 5 people boarded it. At the 2nd stop, 1/2 of the people in it alighted and 20 people boarded the bus. When it left the 2nd stop, there were 60 passengers in it. How many passengers were there in the bus when it left the interchange?
Let number of passengers when it left the interchange, be P
Then, after leaving the 1st stop, number of passengers were: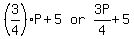 
At the 2nd stop,  got off, and 20 boarded. After leaving the
2nd stop, number of passengers on the bus was: 
Also, number of passengers that remained on the bus was 60.
We then get: 
3P + 20 = 320 ------ Multiplying by LCD, 8
3P = 300
Number of passengers when bus left the interchange, or 
OR
You can determine the original number by working BACKWARDS, as follows:
Number of passengers AFTER leaving 2nd stop: 60
Number of passengers UPON arriving at 2nd stop: 
Number of passengers UPON arriving at 1st stop: 
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
This kind of problem is often easier to solve by working backwards. Here is a solution by that method.
The bus finished with 60 passengers; that was after 20 people boarded it at the second stop. So before those 20 passengers boarded, the number of passengers was 60-20 = 40.
Upon arriving at that second stop, half the passengers got off the bus. Since there were 40 left after half of them got off, the number on the bus upon arriving at the second stop was 40*2 = 80.
At the first stop, 5 passengers got on the bus; so before those passengers got on the bus the number of passengers was 80-5 = 75.
Upon arriving at the first stop, 1/4 of the passengers got off the bus; that means the 75 people on the bus before the other 5 got on was 3/4 of the number that had been on the bus upon arriving at the first stop. 3/4 of 100 is 75, so the original number of passengers, before arriving at the first stop, was 100.
ANSWER: 100
|
|
|
| |
