Question 1202328: A sinusoidal function has an amplitude of 8 units, ad period of 180, and a minimum at (0, -3). Determine the equation of the function.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52858)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A sinusoidal function has an amplitude of 8 units, ad period of 180,
and a minimum at (0, -3). Determine the equation of the function.
~~~~~~~~~~~~~~~~
Since this sinusoidal function has a minimum at x= 0, it tells us
that the pattern is m-a*cos(bx) without a phase shift,
where "m" is the midline, "a" is the amplitude and "b" is the coefficient
managing the period.
About the amplitude, we are given that a= 8; hence, m = 8-3 = 5.
Since the period is 180 units, we have
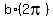 = 180,
so b = = 180,
so b = 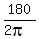 = = 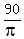 .
Thus and finally, the function is f(x) = .
Thus and finally, the function is f(x) = 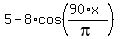 . ANSWER . ANSWER
Solved.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: y = -8cos(2x)+5
This is when we are in degree mode.
Other answers are possible.
================================================================================
Explanation:
The template for cosine is
y = A*cos(B(x-C))+D
where,
|A| = amplitude
B = used to find the period
C = phase shift
D = midline
|A| = 8 leads to either A = 8 or A = -8
Let's go with A = -8 because A = 8 will make x = 0 lead to a max, when we want x = 0 to lead to a min instead.
"period of 180" seems to imply your teacher wants things in degree mode (rather than radians).
T = 180 = period
B = 360/T
B = 360/180
B = 2
To make things simple, I'll have the phase shift be set to C = 0.
One minimum point is located at (0,-3)
The smallest y output possible is y = -3
Go up 8 units, the amplitude amount, to arrive at y = -3+8 = 5 which is the midline
Therefore, D = 5
Summary:
A = -8
B = 2
C = 0
D = 5
y = A*cos(B(x-C))+D
y = -8*cos(2(x-0))+5
y = -8cos(2x)+5
Graph
https://www.desmos.com/calculator/gigkk7becm
GeoGebra is another graphing option I recommend.
|
|
|