Question 1202304: The sum of the squares of two numbers is 218 and their difference multiplied by the smaller number equals 42. Find the two numbers.
Found 4 solutions by math_tutor2020, Edwin McCravy, ikleyn, mccravyedwin:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Answer: The two numbers are 13 and 7
Work Shown:
x and y are the two numbers
Let x > y
I'll assume both are integers.
x^2 + y^2 = 218 ... sum of squares
y^2 = 218 - x^2
y = sqrt(218 - x^2)
x-y = difference
y(x-y) = 42
xy - y^2 = 42
x*sqrt(218-x^2) - (218 - x^2) = 42
x*sqrt(218-x^2) - 218 + x^2 = 42
x*sqrt(218-x^2) - 218 + x^2 - 42 = 0
Use a graphing calculator such as Desmos or GeoGebra to plot
f(x) = x*sqrt(218-x^2) - 218 + x^2 - 42
You should find one of the x intercepts is x = 13
y = sqrt(218 - x^2)
y = sqrt(218 - 13^2)
y = 7
The two numbers are 13 and 7.
Check:
7^2 + 13^2 = 49 + 169 = 218
7*(13-7) = 7*6 = 42
The answers are confirmed.
Answer by Edwin McCravy(20056)  (Show Source):
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
The sum of the squares of two numbers is 218 and their difference
multiplied by the smaller number equals 42. Find the two numbers.
~~~~~~~~~~~~~~~~~~
First equation is
x^2 + y^2 = 218. (1)
Second equation is
y*(x-y) = 42. (2)
We do not see an algebra way to solve it; so, will assume the numbers integer
and will try to solve the problem using the properties of integer numbers.
Using elementary number theory arguments, from equation (1) it is easy to derive
that the numbers x and y should both be odd.
The number 42 has the following odd divisors 1, 3, 7, 21.
So, we write
x^2 = 218 - y^2
and look, which of these values of y will give us the square of integer x
218 - 1^2 = 217 is not a square of an integer
218 - 3^2 = 218 - 9 = 209 is not a square of an integer;
218 - 7^2 = 218 - 49 = 169 is the square of the integer number 13.
218 - 21^2 is negative, so it is not a square, at all.
So, only y= 7 is the appropriate candidate, and with x= 13 it really gives a solution.
Solved.
/////////////////////
I wrote this post as an alternative to the solution by @math_tutor2020;
but now Edwin found the second possible answer, which changed the entire field dramatically.
Edwin, my congratulations - your solution is very nice and very unexpected !
\\\\\\\\\\\\\\\\\\\\\\\
After seeing the solution by Edwin, I quickly got that there is
a straightforward Algebra way to do the same without any tricks.
This way is to express x = 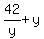 from equation (2) and substitute it into equation (1)
written in the form
 = 218 -  .
It will give a biquadratic equation with four roots for y, that will bring four routs for x.
Answer by mccravyedwin(407)  (Show Source):
You can put this solution on YOUR website!
Two of the above are incomplete because there are two solutions.
Mine (the second one) is the only complete one.
Ikleyn mistook the problem as requiring that the solution be integers.
That was not necessary and caused the second solution to be lost.
The trick to making the algebra simpler was to use the smaller as x
and the larger as x+k where k > 0
Edwin
|
|
|
