Question 1202209: A password must be created using 4 letters from the word "PASSWORD". In how many ways can the letter be arranged?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The third question apparently from the same student in which the meaning of the question is unclear....
Once the 4 letters are chosen, the number of different ways of arranging them is 4! = 24, unless both of the letters S are chosen; in that case the number of arrangements of the 4 letters is 4!/2! = 12.
ANSWER: 12 if both letters S are chosen; 24 otherwise.
-------------------------------------------------------------------------
NOTE: The solution shown by tutor @ikleyn is very likely the question that the problem INTENDED to ask.
However, the wording of the problem implies that 4 letters are chosen from the letters in PASSWORD; and then THOSE 4 LETTERS are arranged.
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A password must be created using 4 letters from the word "PASSWORD".
In how many ways can the  letters be arranged? letters be arranged?
~~~~~~~~~~~~~~~~~~~~~~
In this word "PASSWORD", there are 7 different letters; one letter "S" is repeated twice.
Let's consider first the case, when all 4 letters of a password are different.
There are 7*6*5*4 = 840 such passwords (arranging).
Now consider the opposite case, when two letters in password are "S".
There are  = = 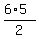 = 3*5 = 15 ways to select the remaining
two letters from 6 = 8-2 letters, different from "S".
Further, this number 15 we should multiply by the number of different arranging of 4 letters,
two of which are identical "S".
So the number of these passwords with two "S" is = 3*5 = 15 ways to select the remaining
two letters from 6 = 8-2 letters, different from "S".
Further, this number 15 we should multiply by the number of different arranging of 4 letters,
two of which are identical "S".
So the number of these passwords with two "S" is 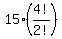 = 15*12 = 180.
In all, we have the number of all possible distinguishable passwords/arranging 840 + 180 = 1020. ANSWER = 15*12 = 180.
In all, we have the number of all possible distinguishable passwords/arranging 840 + 180 = 1020. ANSWER
Solved.
//////////////////
My note to note by @greenestamps
In his post-solution note, tutor @greenestamps writes
NOTE: The solution shown by tutor @ikleyn is very likely the question that the problem INTENDED to ask.
However, the wording of the problem implies that 4 letters are chosen from the letters in PASSWORD; and then THOSE 4 LETTERS are arranged.
The wording of the problem DOES NOT implies that 4 letters are just chosen.
To assert this is to pervert the problem.
He solves the problem in his interpretation; me - in my interpretation.
The fact that two different interpretations are possible means
a crash, a catastrophe and a death sentence for this problem,
as it is written in the post.
........................
Obviously, the person who created this problem, is unprofessional Math composer
and creates his compositions " kneeling in the garage ", even without reading any Math textbooks
and learning Math exclusively from reading this and other Internet web-sites.
A correctly worded and the ONLY POSSIBLE question should be " how many different passwords are possible ? "
|
|
|