SOLUTION: The question writes: “There are 8 keys split between two key rings with at least 2 keys on each ring. Both key rings can be rotated or turned over. How many different ways can th

If this problem is given to a student, it assumes that the student is just familiar with

    - combinations;
    - circular permutations;
    - and the Fundamental counting principle.


These are pre-requisites.


So, I may assume that you know about the number of permutations   = ,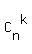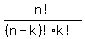

and you know about the number of circular permutations of m objects (m-1)!



Then the solution of the problem is not too hard and you can understand it.


Let k be an integer number between 2 and 6, inclusive:  2 <= k <= 6.


Then you have 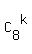   ways to select "k" key on the 1st ring; the rest (8-k) keys
automatically will go to the second ring.


There are (k-1)! circular permutations of  "k"  keys on the 1st ring and 
(8-k-1)!  circular permutations of  (8-k)  keys on the 2nd ring.


For now, it gives 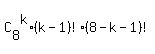   possible ways placing the keys.
But my reasoning is not completed, yet.


Turning 1st ring DOES NOT CHANGE the number of placing the keys on the 1st ring;
all possible placing are just accounted for by the formula (k-1)!

Turning 2nd ring DOES NOT CHANGE the number of placing the keys on the 2nd ring;
all possible placing are just accounted for by the formula (8-k-1)!

So, the above formula still remains with no change, even although the turnings are accounted.


Finally, you should make the sum of these addends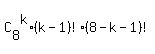    
over all "k" from 2 to 6, inclusive.


Thus, your final formula is

    number of placing = .     (1)


At this point, I completed my explanations. If you want to get the value,
make calculations on your own, following this remarkable formula (1),
which I developed for you with all necessary auxiliary explanations.