Question 1202157: Two chords, AD and BC of a circle intersect at a point O inside the circle. Given that BO=5cm, OD=3cm and CD=3.6 cm, calculate the length AB
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Two chords, AD and BC of a circle intersect at a point O inside the circle.
Given that BO = 5 cm, OD = 3 cm and CD = 3.6 cm, calculate the length AB.
~~~~~~~~~~~~~~~
Make a sketch, drawing the circle, the chords and marking the points.
Consider triangles AOB and DOC.
These triangles are similar.
Indeed, their angles AOB and DOC are congruent, since they are vertical angles.
Angles BAO and OCD are congruent, too, because the angles BAD and BCD are inscribed angles
leaning on the same arc BD of the circle.
It is just enough for the proof that triangles AOB and DOC are similar, having two pairs
of congruent angles.
From the triangle similarity, the corresponding pairs of sides are (BO,OD) and (AB,CD),
so we can write a proportion
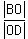 = = 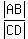 .
Substituting the values, we get .
Substituting the values, we get
 = = 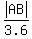 .
It gives AB = .
It gives AB = 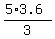 = =  = 6.
ANSWER. AB = 6 cm. = 6.
ANSWER. AB = 6 cm.
Solved.
|
|
|