Question 1202133: A labor rights group wants to determine the mean salary of app-based drivers. If she knows that the standard deviation is $3.9, how many drivers should she consider surveying to be 98% sure of knowing the mean will be within
?
143
39
12
2168
19
Answer by Theo(13342)   (Show Source): (Show Source):
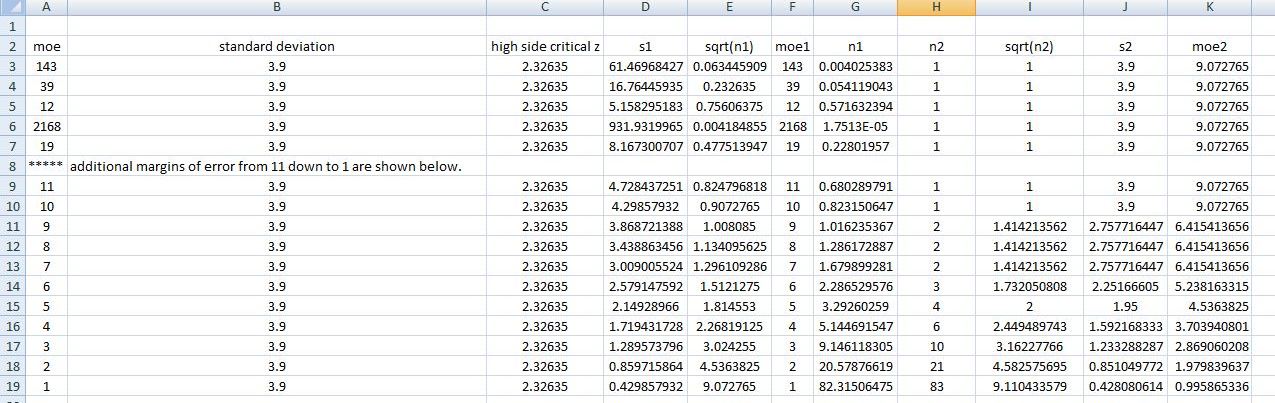
You can put this solution on YOUR website! what i find is that the minimum sample size is 1 for all of margin of error selections you provided.
the margin of error in all of them will be equal to 9.072765.
the margin of error will be equal to 9.072765 until the required margin of error is less than that.
this occurs in the spreadsheet when the required margin of error is equal to 9 or less.
i used excel to profided calculated margins of error when the required margin of error was equal to the ones provided, plus when the reuired margin of error was equal to 11 or less.
as indicated in the excel spreadsheet the minimum sample size doesn't get greater than 1 until the required margin of error is equal to 9 or less.
without going into the details, what you should get out of this is:
if you calculate the square root of the sample size, and use that directly, you will get exactly the margin of error you are looking for, based on the formulas provided.
once you square the square root of the sample size and then round it up to the next highest integer, and then use the square root of that rounded up sample size, you will get a margin of error that is slightly less than the desired margin of error.
in all the selections that you provided, the required sample size doesn't get greater than 1 until you require a margin of error less than 9.072765.
that first occurred when the reuired margin of error was equal to 9 in the excel spreadsheet.
since the square root of 1 is equal to 1, you got the margin of error equal to 2.32635 * 3.9 = 9.072765 for all margins of error where the sample size, rounded up to the next integer, was equal to 1.
.
|
|
|