Question 1202129: The functions f(theta) and g(theta) are sine functions, where f(theta)=g(theta)=0. The amplitude of f(theta) is twice the amplitude of g(theta). The period of f(theta) is one-half the period of g(theta). If g(theta) has a period of 2pi and f(pi/4)=4. Write the function rule for g(theta). Explain your reasoning.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52844)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The functions f(theta) and g(theta) are sine functions, where  f(0) = g(0) = 0. f(0) = g(0) = 0.
The amplitude of f(theta) is twice the amplitude of g(theta).
The period of f(theta) is one-half the period of g(theta).
If g(theta) has a period of 2pi and f(pi/4)=4. Write the function rule for g(theta).
Explain your reasoning.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Notice that I changed/edited your post
by guiding my common sense and the context.
Also, in this situation, there is no need to torture yourself, writing "theta" everywhere,
when it is possible to replace it by short variable "x".
According to the problem, functions g(x) is sinusoidal, has the value of 0 at x= 0
and has a period  . Hence, g(x) has the form
g(x) = . Hence, g(x) has the form
g(x) = 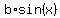 , where real number "b" is the amplitude of g(x).
Function f(x) is sinusoidal, has the value of 0 at x= 0 and has a period, which is
one-half of that of g(x), i.e. , where real number "b" is the amplitude of g(x).
Function f(x) is sinusoidal, has the value of 0 at x= 0 and has a period, which is
one-half of that of g(x), i.e.  . Hence, f(x) has the form
f(x) = . Hence, f(x) has the form
f(x) = 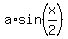 , where real number "a" is the amplitude of f(x).
Next, we are given , where real number "a" is the amplitude of f(x).
Next, we are given  = 4. It means = 4. It means 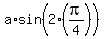 = 4, or = 4, or 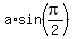 = 4.
Since = 4.
Since 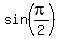 = 1, it gives us a = 4.
It implies, due to the problem description, that the amplitude of g(x) is 2 : b = 2.
Thus g(x) has the form
g(x) = = 1, it gives us a = 4.
It implies, due to the problem description, that the amplitude of g(x) is 2 : b = 2.
Thus g(x) has the form
g(x) = 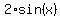 . ANSWER . ANSWER
Solved.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The period of g is 2pi, and the period of f is half the period of g, so the period of f is pi.
f(0) and g(0) are both zero, so theta=0 is the beginning of a period for both f and g.
Since theta = 0 is the beginning of a period for f, which has a period of pi, theta = pi/4 is 1/4 of the way through a period. A sine function is at its maximum 1/4 of the way through a period, so the maximum value of f is f(pi/4)=4.
That means the amplitude of f is 4; and since the amplitude of f is twice the amplitude of g, the amplitude of g is 2.
So g has ampitude 2 and period 2pi; the function is g = 2sin(theta).
ANSWER: g = 2sin(theta)
|
|
|