What is xx2? Do you mean  ? If not, please correct and re-post.
? If not, please correct and re-post.
If you DID MEAN to write  then:
then:
f'(x) = 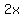
f"(x) =  <<< constant positive value so concave up "everywhere"
<<< constant positive value so concave up "everywhere"
which of course includes [-4,6]
A. It is not concave down at all on [-4,6]
B. It is concave up on [-4,6]
C. There is no inflection point on [-4,6] (or otherwise)
D. The minimum is at x=0 (set f' = 0, solve for x)
E. The maximum on [-4,6] occurs at x=6 (you check at the endpoints of the interval [-4,6]: f(-4) = 20, f(6) = 40. Since no local maximums occur within the interval [-4,6] (rememmber it is concave up so you can only have a local minimum), there are no critical points to check on (-4,6) )